§ 2. Задача безусловной оптимизации

Здесь мы введем основные понятия и проведем теоретическое исследование задачи безусловной оптимизации. Отметим, что эта задача в теоретическом плане достаточно полно изучена в курсе математического анализа. Мы лишь повторим важнейшие факты, обращая внимание на "оптимизационную" специфику.

2.1. Определения.

Итак, мы будем рассматривать задачу безусловной оптимизации

f(x) → min,

(1)

где f: R^m → R. Точка x* ∈ R^m называется решением задачи (1) (или точкой глобального безусловного минимума функции f), если

f(x*) ≤ f(x)

(2)

при всех x ∈ Rm. Если неравенство (2) выполнено лишь для x, лежащих в некоторой окрестности Vx* точки x*, то точка x* называется локальным решением задачи (1), или точкой локального безусловного минимума функции f. Если неравенство (2) строгое при всех x ≠ x*, то говорят о строгом глобальном и, соответственно, строгом локальном минимумах. Решение задачи (1) иногда обозначают argmin f(x) (или, более полно, argminx∈Rm f(x); когда речь идет о задачах безусловной оптимизации в обозначениях argminx∈Rm f(x) и minx∈Rm f(x) мы будем всегда опускать индекс "x ∈ Rm"). Обычно из контекста ясно о каком минимуме (локальном, глобальном и т. д.) идет речь.

Аналогичные понятия (максимумов) определяются для задачи

f(x) → max.

З а д а ч а  2.1. Докажите, что точка x* является точкой глобального безусловного (соответственно, локального, строгого) максимума функции f в том и только том случае, когда она является точкой глобального безусловного (соответственно, локального, строгого) минимума функции –f.

Поэтому всюду в дальнейшем мы будем заниматься только задачами о минимумах, все время помня, что задачи о максимумах к ним сводятся. Таким образом, слово "оптимизация" в нашем контексте будет всегда синонимом слова "минимизация".

2.2. О линейных операторах в R^m.

Напомним, что линейный оператор A в R^m называется самосопряженным или симметричным, если при всех x, y ∈ R^m

(Ax, y) = (x, Ay).

Известно, что оператор A симметричен в том и только том случае, когда его матрица симметрична (т. е.переходит в себя при транспонировании).

Оператор A называется невырожденным, если у него нулевое ядро ker A, т. е. если он переводит в нуль только нуль. Другими словами, уравнение Ax = Θ имеет только нулевое решение. Из курса алгебры известно, что оператор A невырожден в том и только том случае, если определитель его матрицы отличен от нуля.

Оператор A называется положительно определенным (часто пишут A > 0), если

(Ax, x) > 0

при всех ненулевых x ∈ R^m. В соответствии с критерием Сильвестра оператор A положительно определен в том и только том случае, если все главные диагональные миноры матрицы оператора A положительны. Наконец, оператор A называется неотрицательно определенным (пишут A ≥ 0), если при всех x ∈ R^m

(Ax, x) ≥ 0.

Аналогично определяются понятия отрицательно и неположительно определенных операторов.

Если оператор A – λI, где I — тождественный оператор на R^m, а λ ∈ R, положительно (неотрицательно) определен, то часто пишут A > λ (соответственно, A ≥ λ). Аналогично определяются записи A < λ и A ≤ λ.

Из курса алгебры известно, что симметричный оператор A удовлетворяет неравенствам

λ ≤ A ≤ Λ,

в том и только том случае, если все точки спектра σ(A) оператора A лежат на отрезке [λ, Λ]:

λ ≤ λi ≤ Λ.

(3)

В частности, поскольку норму в R^m мы считаем евклидовой, для симметричных операторов A имеют место утверждения

||A|| =  max λi∈σ(A) {|λi|} ≤ max{|λ|, |Λ|}.

(4)

2.3. О дифференцируемости функций на R^m.

Напомним ряд понятий и фактов из курса математического анализа, которые потребуются нам в дальнейшем.

Вектор a ∈ R^m такой, что

f(x + h) – f(x) – (a, h) = o(h)

при всех h ∈ R^m называется производной или градиентом функции f в точке x. Здесь и ниже символ o(h) обозначает произвольную функцию, обладающую свойством

o(h) ||h||  → 0 при h→ Θ.

Функция f называется при этом дифференцируемой в точке x. Градиент обычно обозначается f ′(x), или grad f(x), или ∇f(x). Мы будем, как правило, использовать первое обозначение. Известно, что в координатной форме градиент имеет вид

f ′(x) =  ( ∂f(x) ∂x1 , ...,  ∂f(x) ∂xm )  =  ( ∂f(x1, ..., xm) ∂x1 , ...,  ∂f(x1, ..., xm) ∂xm ) .

Функция f: R^m → R^m дифференцируемая в каждой точке называется дифференцируемой.

Если дополнительно найдется линейный самосопряженный оператор A: R^m → R^m такой, что при всех h ∈ R^m

f(x + h) – f(x) – (f ′(x), h) –  1 2 (Ah, h) = o(h2),

где запись o(h²) означает, что

o(h2) ||h||2  → пpи h→ Θ,

то f называется дважды дифференцируемой в точке x, а оператор A называется второй производной функции f в точке x и обозначается f ′′(x) либо ∇²f(x). Матрицей, отвечающей оператору A = f ′′(x), служит, как нетрудно видеть, так называемая матрица Гессе или гессиан функции f:

A =  ⌈ | | | | | | | | | ⌊ ∂2f(x) ∂x1∂x1 ··· ∂2f(x) ∂x1∂xm : ··· : ∂2f(x) ∂xm∂x1 ··· ∂2f(x) ∂xm∂xm ⌉ | | | | | | | | | ⌋ .

З а д а ч а  2.2*. Пусть A — линейный самосопряженный оператор в R^m, b ∈ R^m, c ∈ R и f(x) = (Ax, x)/2 + (b, x) + c. Докажите, что f ′(x) = Ax + b, и f ′′(x) = A.

Если функция F: R^m → R^k, то линейный оператор A: R^m → R^k такой, что

F(x + h) – F(x) – Ah = o(h)

называется производной функции F в точке x и обозначается F ′(x) (это обобщение понятия градиента на случай функций со значениями в R^k).

Если функция F: R^m → R дифференцируема, то ее градиент можно рассматривать как функцию из R^m в R^m: каждому x ∈ R^m ставится в соответствие точка из f ′(x) ∈ R^m.

З а д а ч а  2.3*. Докажите, что [f ′(x)]′ = f ′′(x). Поясним: здесь [f ′(x)]′ — производная функции x → f ′(x), действующей из R^m в R^m, а f ′′(x) — вторая производная функции f: R^m → R^m.

Еще одно полезное понятие. Функция F: R^m→ R^k по определению удовлетворяет условию Липшица с константой Λ, если при всех x, y ∈ R^m

||F(x) – F(y)|| ≤ Λ ||x – y||.

З а д а ч а  2.4*. Пусть F: R^m →R^k дифференцируема. Докажите, что F удовлетворяет условию Липшица с константой Λ, в том и только том случае, если ||F ′(x)|| ≤ Λ при всех x.

Ниже нам потребуется следующее простое утверждение. Если f: R^m → R — дважды непрерывно дифференцируемая функция, то для того, чтобы ее градиент f ′ удовлетворял условию Липшица с константой Λ необходимо и достаточно, чтобы при всех x ∈ R^m выполнялось неравенство f ′′ ≤ Λ. Действительно, в силу задачи 2.3 при всех t ∈ R и x, h ∈ R^m

(f ′(x + th), th) – (f ′(x), th) = (f ′′(x)th, th) + (o(th), th).

Но тогда в силу условия Липшица для f ′

(f ′′(x)h, h) ≤  1 t2 |(f ′(x + th) – f ′(x), th)| +  |o(th, th)| t2  ≤

≤  Λ||th||2 t2  +  ||o(th)|| · ||th|| t2  = Λ ||h||2 +  ||o(th)|| t ||h||.

Устремляя t к 0, получим неравенство

(f ′′(x)h, h) ≤ Λ ||h||2,

(5)

эквивалентное нужному неравенству f ′′(x) ≤ Λ.

З а д а ч а  2.5. Докажите обратное утверждение.

В заключение пункта еще одно обозначение. Мы будем писать f ∈ C, f ∈ C¹ и f ∈ C², если f соответственно непрерывна, непрерывно дифференцируема и дважды непрерывно дифференцируема.

2.4. Необходимое условие локального экстремума.

Такое условие дает хорошо известная из курса математического анализа

Теорема Ферма. Если f — дифференцируемая функция и x* — ее локальный минимум, то f ′(x*) = 0.

Напомним  д о к а з а т е л ь с т в о  теоремы. Допустим противное: f ′(x*) ≠ Θ. Положим x_t = x* – tf ′(x*) для всех t > 0. Тогда, во-первых, очевидно, x_t – x* → Θ при t → 0 и, во-вторых, по определению градиента,

f(xt) = f(x*) + (f ′(x*), xt – x*) + o(xt – x*) = = f(x*) + (f ′(x*), –tf ′(x*)) + o(–tf ′(x*)) = = f(x*) –  [ ||f ′(x*)||2 +  o(–tf ′(x*)) t ] .

(6)

Поскольку ||f ′(x*)|| > 0, а

o(–tf ′(x*)) t  = ||f ′(x*)||· o(–tf ′(x*)) ||(–tf ′(x*)||  → 0 пpи t→ 0,

выражение в квадратных скобках в правой части (6) при всех достаточно малых t положительно и поэтому при всех достаточно малых положительных t

f(xt) < f(x*),

что противоречит тому, что x* = argmin f(x).

Из доказательства следует, что, двигаясь из заданной точки в направлении, противоположном градиенту (говорят в направлении антиградиента), мы локально уменьшаем значение функции. Это замечание потребуется нам в дальнейшем.

Таким образом, минимум функции может достигаться только в тех точках, в которых ее производная обращается в нуль, и поэтому уравнение

f ′(x) = 0,

(7)

или, что то же самое, система m (вообще говоря, нелинейных) уравнений с m неизвестными

∂f(x1, ..., xm) ∂xi  = 0,   i = 1, ..., m,

определяет точки "подозрительные на минимум". Точки, удовлетворяющие уравнению (7), называются стационарными точками функции f.

Стационарная точка x* функции f может быть либо точкой локального минимума, либо точкой локального максимума, либо не быть ни той, ни другой (см. рис. 1).

Рис. 1.

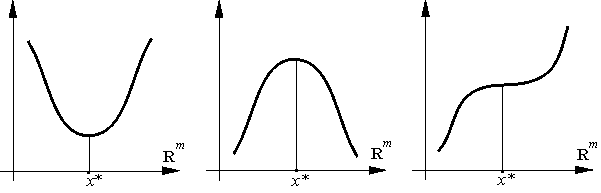
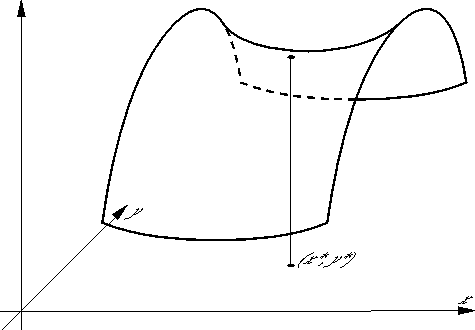
f(x*, y) ≤ f(x*, y*) ≤ f(x, y*)

(см. рис. 2). Если эти неравенства выполняется лишь для x достаточно близких к x* и y достаточно близких к y*, то, естественно, добавляется эпитет локальная.

Рис. 2.

2.5. Теорема о локальном минимуме (необходимые и достаточные условия второго порядка).

Пусть x* — стационарная точка дважды дифференцируемой функции f. Для того, чтобы точка x* была точкой (локального) минимума функции f необходимо, чтобы оператор f ′′(x*) был неотрицательно определен и достаточно, чтобы он был положительно определен.

Д о к а з а т е л ь с т в о. Необходимость. Пусть x* — точка минимума и h — произвольный вектор из R^m. Поскольку (в силу теоремы Ферма) x* — стационарная точка,

0 < f(x* + th) – f(x*) =  1 2 (f ′′(x*)th, th) + o((th)2)

при всех достаточно малых t ∈ R. Отсюда при всех t ≠ 0

(f ′′(x*)h, h) +  o((th)2) t2  > 0.

Переходя в полученном неравенстве к пределу при t→ 0 и учитывая, что как легко видеть, o((th)²)/t² → 0 при t → 0, получим нужное неравенство

(f ′′(x*)h, h) ≥ 0.

Достаточность. Пусть f ′′(x*) положительно определен, а стационарная точка x* не является точкой локального минимума. Последнее означает наличие последовательности x ⁿ→ x* при n → ∞ такой, что f(xⁿ) < f(x*). Положим hⁿ = xⁿ – x*. По определению второй производной, учитывая, что x* стационарна,

0 > f(x* + thn) – f(x*) =  1 2 (f ′′(x*)hn, hn) + o((hn)2).

Если теперь обозначить hⁿ/||hⁿ|| через gⁿ, то последнее неравенство (поделив его на ||hⁿ||²) можно переписать в виде

(f ′′(x*)gn, gn) +  o((hn)2) ||hn||2  < 0.

(8)

Поскольку ||gⁿ|| = 1, а сфера в R^m компактна, последовательность {gⁿ}, не ограничивая общности, можно считать сходящейся к некоторому лежащему на ней (и следовательно, отличному от нуля) вектору g⁰. Предельный при n → ∞ переход в неравенстве (8) приводит к противоречащему положительной определенности оператора f ′′(x*) неравенству

(f ′′(x*)g0, g0) ≤ 0.

Теорема доказана.

З а д а ч а  2.6. Исследуйте на экстремум функцию f: R2 → R, задаваемую формулой f(x1, x2) = x12/a+ x22/b,при различных a и b.

2.6. Замечания о существовании решений.

Из курса математического анализа известно, что задача о существовании минимума непрерывной функции на компактном множестве всегда имеет по крайней мере одно решение (теорема Вейерштрасса). В нашем случае — случае некомпактной области определения — нужны дополнительные условия.

З а д а ч а  2.7. Приведите пример задачи (1) с непрерывной (или, даже, со сколь угодно гладкой) ограниченной снизу (f(x) ≥ l при некотором l и всех x ∈ R^m) функцией f, не имеющей решения.

В следующей теореме приводится одно из таких возможных дополнительных условий.

Теорема о разрешимости задачи безусловной оптимизации. Пусть функция f непрерывна и при некотором α ∈ R^m множество S_α = {x ∈ R^m: f(x) ≤ α} непусто и ограничено. Тогда задача (1) имеет по крайней мере одно решение.

Д о к а з а т е л ь с т в о. Множество S_α замкнуто.

З а д а ч а  2.8*. Докажите.

Поэтому Sα — компактное подмножество Rm. В силу теоремы Вейерштрасса, очевидно, функция f достигает на Sα своего минимума: x* = argminx∈Sα f(x). Очевидно, x* — решение задачи (1), поскольку f(x*) ≤ α в Sα, а вне Sα функция f принимает значения бóльшие α.

З а д а ч а  2.9. Приведите пример (непостоянной) функции f, для которой задача (1) разрешима, а условия теоремы 2.6 не выполнены.

2.7. Замечания о единственности решений.

Вопрос о единственности (как, впрочем, и о существовании) решений весьма важен в теоретическом плане. Например, если x* — единственное решение задачи (1) и {x^k} ⊂ R^m — ограниченная последовательность такая, что f(x^k) → f(x*) = min f(x) при k→ ∞, то x^k → x* = argmin f(x) при k → ∞. Такое свойство бывает полезным при исследовании приближенных методов решения оптимизационных задач.

З а д а ч а  2.10. Докажите сформулированное утверждение (воспользуйтесь компактностью последовательности {x^k}).

Точка x* локального минимума дважды дифференцируемой функции f называется невырожденной, если оператор f ′′(x*) невырожден. Она называется локально единственной, если в некоторой ее окрестности V_x* нет других точек локального минимума функции f.

З а д а ч а  2.11. Приведите пример функции f, имеющей локально строгую, но не локально единственную точку минимума.

Теорема о локальной единственности решений. Невырожденная точка локального минимума локально единственна.

Д о к а з а т е л ь с т в о. Допустим противное: x* не является локально единственной точкой минимума, т. е. найдется сходящаяся к x* последовательность {xⁿ} локальных минимумов функции f. Тогда (см. задачу 2.3)

f ′(xn) – f ′(x*) = f ′′(x*)(xn –x*) + o(xn – x*).

Поскольку xⁿ и x* — локальные минимумы и, следовательно, стационарные точки, f ′(xⁿ) = f ′(x*) = Θ. Далее, положим (как мы уже делали) gⁿ = (xⁿ – x*)/||xⁿ – x*||. Тогда, очевидно,

f ′′(x*)gn =  o(xn – x*) ||xn – x*|| .

(9)

Далее рассуждения стандартны: {gⁿ} лежит на единичной сфере в R^m, поэтому ее можно считать сходящейся к некоторому пределу g ⁰ ≠ Θ. Переходя к пределу в (9), получаем

f ′′(x*)g0 = Θ,

что противоречит невырожденности оператора f ′′(x*).

З а д а ч а  2.12. Восстановите детали доказательства.

2.8. Выпуклые функции на R^m.

Особенно легко вопросы существования и единственности решаются для выпуклых функций. Эти функции являются очень важным объектом в теории оптимизационных задач. Начнем с определений.

Функция f: R^m → R называется выпуклой, если при всех x, y ∈ R^m и λ ∈ (0, 1)

f(λx + (1 – λ)y) ≤ λf(x) + (1 – λ)f(y).

(10)

Если неравенство (10) строгое, то f называется строго выпуклой. Геометрически выпуклость означает, что график функции на интервале (x, y), соединяющем любые точки x и y, лежит не выше прямой, соединяющей точки (x, f(x)) и (y, f(y)) (см. рис. 3а). Функция f сильно выпукла (с константой c > 0), если неравенство (10) выполняется в следующей более сильной форме

f(λx + (1 – λ)y) ≤ λf(x) + (1 – λ)f(y) +  c 2 λ(1 – λ)||x – y||2.

(11)

Рис. 3.

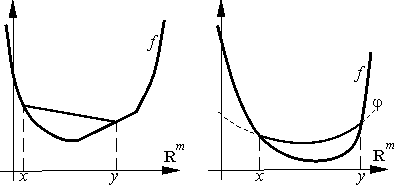
Геометрически это понятие можно интерпретировать так. Пусть точки отрезка [x, y], соединяющего точки x и y, параметризованы параметром λ: λ → λx + (1 – λ)y. Правая часть неравенства (11) определяет на этом отрезке полином φ второго порядка (от λ). График сильно выпуклой функции над отрезком [x, y] должен лежать ниже параболы — графика этого полинома (см. рис. 3б).

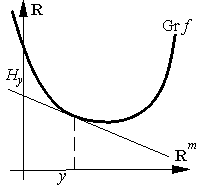
Критерий выпуклости дифференцируемой функции. Для того, чтобы дифференцируемая функция f была выпуклой необходимо и достаточно выполнения при всех x, y ∈ R^m неравенства

f(x) – f(y) ≥ (f ′(y), x – y).

(12)

Действительно, определим на отрезке [0, 1] функцию φ, положив

φ(λ) = f(λx + (1 – λ)y).

Очевидно функция φ выпукла одновременно с функцией f. Кроме того, легко показать, что

φ′(λ) = (f ′(λx + (1 –λ)y), x – y).

Неравенство (12) в новых обозначениях переписывается в виде

φ(1) – φ(0) ≥ φ′(0),

или, если воспользоваться формулой Лагранжа,

φ′(τ) ≥ φ′(0),

(13)

где τ — некоторая точка интервала (0, 1). Из курса математического анализа известно, что для дифференцируемых функций выпуклость эквивалентна монотонности производной. Поэтому, если f выпукла, то φ′ монотонна. Следовательно, имеет место эквивалентное (12) неравенство (13).

З а д а ч а  2.13. Докажите обратное утверждение.

Геометрически доказанное утверждение означает, что значения функции f(x) "лежит выше" гиперплоскости H_y = {(x, ξ) ∈ R^m×R: ξ = f(y) + (f ′(y), x – y)}, касательной в точке (y, f(y)) к графику Gr f = {(x, ξ) ∈ R^m× R: ξ = f(x)} при всех y ∈ R^m (см. рис. 4).

Рис. 4.

Строгая выпуклость дифференцируемой функции, как легко видеть, эквивалентна строгому при x ≠ y неравенству (12). Сильная же выпуклость функции f эквивалентна выполнению при всех x и y неравенства

f(x) – f(y) ≥ (f ′(y), x – y) + c||x – y||2.

(14)

З а д а ч а  2.14*. Докажите последнее утверждение.

З а д а ч а  2.15*. Докажите, что f ∈ C² сильно выпукла с константой c в том и только том случае, если f ′′(x) ≥ c при всех x ∈ R^m.

2.9. Теорема о разрешимости для сильно выпуклой функции.

Задача (1) с дифференцируемой сильно выпуклой функцией разрешима.

Д о к а з а т е л ь с т в о. Неравенство (14) для y = Θ и произвольного x имеет вид

f(x) ≥ f(Θ) + (f ′(Θ), x) +c||x||2.

(15)

Для α = f(Θ) множество S_α = {x ∈ R^m: f(x) ≤ α}, во-первых, непусто, поскольку содержит точку Θ, а во-вторых, ограничено, поскольку вне шара B(Θ, ||f ′(Θ)||/c)

f(x) > α.

Действительно, продолжая (15), при ||x|| > ||f ′(Θ)||/c имеем

f(x) ≥ f(Θ) + (f ′(Θ), x) + c||x||2 ≥ α – |(f ′(Θ), x)| + c||x||2 ≥ ≥ α + c||x||2 – ||f ′(Θ)|| · ||x|| = α + ||x||(c||x|| – ||f ′(Θ)||) > α.

Заключение теоремы теперь следует из теоремы 2.6 о разрешимости задачи безусловной оптимизации.

З а д а ч а  2.16. Покажите, что для выпуклой (и даже для строго выпуклой) функции утверждение теоремы в общем случае не верно.

2.10. Теорема единственности для строго выпуклой функции.

Задача (1) со строго выпуклой функцией не может иметь более одного решения.

Д о к а з а т е л ь с т в о. В предположении существования двух точек минимума x* и x** (очевидно тогда, что f(x*) = f(x**)), в силу строгой выпуклости, получим противоречащее равенству x* = argmin f(x) неравенство

f ( x* + x** 2 )  <  f(x*) 2  +  f(x**) 2  = f(x*).

File based on translation from T_EX by T_TH, version 3.05.
Created 4 Jun 2002, 22: 42.