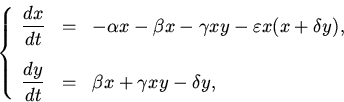Об одной модификации системы ``жертва-патоген'' ¹

Денисова Ю.К., Недорезов Л.В.
Инстиут молекулярной биологии и биофизики СО РАМН, Новосибирск
Бахвалов С.А.
Институт систематики и экологии животных СО РАН, Новосибирск

Рассматривается математическая модель динамики численности двух взаимодействующих популяций ``жертва-патоген''. Она представлена следующей системой дифференциальных уравнений:

$\begin{displaymath} \left\{ \begin{array}{lcl}\displaystyle \frac{dx}{dt} & = &... ... & = & \beta x + \gamma xy - \delta y, \\ \end{array} \right. \end{displaymath}$

(1)

где

- численность здоровых особей в момент времени

- численность больных.

Размножение происходит в фиксированные моменты времени $(t_k - t_{k-1} = h \equiv const > 0)$ по следующему закону:

$\begin{displaymath} \left\{ \begin{array}{lcl} x(t_k) & = & x_k = Y x(t_k - 0), \\ [2mm] y(t_k) & = & y_k = 0, \\ \end{array} \right. \end{displaymath}$

(2)

где

- численность популяции в момент времени перед появлением новой генерации (численность выживших особей, которые могут дать потомство),

- коэффициет размножения (среднее число потомков, порождаемых каждой выжившей особью).

Так же мы предполагаем, что существуют моменты времени : ( $t_{k} < u_{k} < t_{k+1})$ , в которых численность популяции меняется по закону:

$\begin{displaymath} \left\{ \begin{array}{lcl} x(u_{k}) = p x(u_{k} - 0), \\ [2mm] y(u_{k}) = 0, \\ \end{array} \right. \end{displaymath}$

(3)

где $p \in (0,\,1]$ .

Биологически это означает, что по прохождению какого-то промежутка времени (которое в данной модели считается величиной малой), численность здоровых особей уменьшается, а все больные особи погибают. Это является моделью воздействия зимних погодних условий на численность популяции.

Решения модели (1)-(3) неотрицательны при неотрицательных начальных данных и ограничены. Существует устойчивый инвариантный компакт $\Delta$ такой, что если $\left( x(0),\,y(0) \right) \in \Delta$ , то тогда при любом $t > 0,\quad \left(x(t),\,y(t) \right) \in \Delta$ .
При выполнении условия $Y p e^{ - (\alpha + \beta )h} < 1$ популяция вырождается при любых начальных значениях численности.

Численный анализ модели показывает, что в рамках рассматриваемой модели кроме режима вырождения реализуется также режим стабилизации на единственном глобально устойчивом уровне. Важно отметить, что с ростом величины плодовитости стабильный уровень повышается до некоторого конечного значения, а в дальнейшем рост этой величины приводит к снижению уровня. При достижении минимума стабильная точка теряет устойчивость, но возникают дополнительные стационарные состояния (триггерный режим): в зависимости от начальных значений численности система стабилизируется на одном из двух устойчивых уровней. Дальнейшее увеличение величины приводит к тому, что стационарные точки теряют устойчивость и в системе возникают циклические режимы. Таким образом, в относительно простой модели (1)-(3) динамики системы фитофаг-патоген реализуются режимы, сходные по своему характеру с режимами массовых размножений лесных насекомых-фитофагов.

Примечание

... ``жертва-патоген''¹: Работа поддержана грантом РФФИ 93-04-49583.

Ваши комментарии

[Головная страница]
[Конференции]
[СО РАН]

© 2001, Сибирское отделение Российской академии наук, Новосибирск
© 2001, Объединенный институт информатики СО РАН, Новосибирск
© 2001, Институт вычислительных технологий СО РАН, Новосибирск
© 2001, Институт систем информатики СО РАН, Новосибирск
© 2001, Институт математики СО РАН, Новосибирск
© 2001, Институт цитологии и генетики СО РАН, Новосибирск
© 2001, Институт вычислительной математики и математической геофизики СО РАН, Новосибирск
© 2001, Новосибирский государственный университет
Дата последней модификации Saturday, 08-Sep-2001 21:14:14 NOVST

Об одной модификации системы ``жертва-патоген'' 1

Примечание

Об одной модификации системы ``жертва-патоген'' ¹