
Логические средства поддержки информационных технологий
О. А. Ильичева
Ростовский государственный университет
Аннотация:
Предлагаются средства в эффективно исполнимом логическом языке для
представления задач и свойств различных предметных областей. Язык
включает отрицания, равенства, модули. Семантика языка допускает
точную диагностику логических ошибок. Рассматриваются
математические аспекты, обосновывающие подход.
Effectively executable logical tools are offered to represent the
tasks and properties of different subject fields. Logical language
includes negations, equality, modules. The semantics of this
language allows making exact diagnosis of logical mistakes.
Mathematical aspects are considerate to ground the approach.
Интенсивное развитие систем и технологий информационной поддержки
различного рода практических задач обострило проблему
достоверности создаваемых продуктов -- их соответствия
поставленной цели. Даже в такой формализованной области, как
реляционные базы данных, по признанию специалистов, "современная
технология БД обеспечивает слабые возможности для поддержки и
оценки непротиворечивости данных" (СУБД, 4, 1997). Формальные
средства, широко используемые для представления знаний, в
экспертных системах, логическом программировании, не всегда
адекватны для задач анализа и обеспечения корректности
производимых систем. Модели термов, лежащие в основе семантики
традиционных логических языков, не позволяют привычно работать с
равенством, диагностировать даже такие "простые" логические
ошибки, как противоречие, переопределение, неопределенность
функций и т.п. Между тем, именно логический аппарат, на наш
взгляд, является наиболее подходящим средством для таких задач,
как анализ состоятельности проектных решений и оценка последствий
предпринимаемых действий, поддержка непротиворечивости хранимой
информации и корректности модификаций -- т.е. обеспечение
"правильности" работы сложно устроенных систем, чья статическая
или динамическая структура представляет собой запутанный
"клубок" зависимостей и взаимодействий разнородных элементов.
Для этих целей можно использовать достаточно простой логический
язык, но более выразительный, чем версии Пролога, со специально
подобранной эффективной семантикой.
В работе предлагаются средства в эффективно исполнимом логическом
языке для представления широкого спектра задач и свойств различных
предметных областей. Комплекс средств и реализующих их
инструментов включает, в частности:
- язык в исчислении предикатов первого порядка; основное отличие
от Пролога и его аналогов -- возможность использования модулей,
отрицаний, равенства, ограниченных кванторов и переменных сорта
"время" в предложениях; семантика языка допускает не только
эффективную реализуемость, но и точную диагностику логических
ошибок;
- интерпретаторы, осуществляющие логический вывод и проверку
истинности формальных спецификаций на моделях предметной области;
- сборщики модулей с анализом соответствия input-output параметров
и непротиворечивости совокупной спецификации;
- динамические генераторы новых спецификаций в зависимости от
изменяющихся параметров среды.
Эти средства образуют инструментальную среду для автоматизации
создания, модификации и сопровождения различных программных систем
и поддерживают решение следующих задач:
- проектирования -- логическое представление и анализ предметной
области, быстрое создание действующих прототипов с целью раннего
обнаружения ошибок проекта и оценки затрат ресурсов;
- обработки данных и генерации гетерогенных систем в
распределенной среде -- логический анализ и проверка
непротиворечивости представления различных форматов данных и
запрашиваемых свойств;
- технологии многомерной объектно-ориентированной структуризации
-- проверка осуществимости интеграции требуемой конфигурации из
заданной базовой;
- преобразования (декомпозиции, анализа, синтеза и модификаций)
программ -- внутреннее представление графов управления и
зависимостей данных и правил их трансформаций;
- обучения, дистанционного обучения и создания обучающих систем
-- логическое представление баз знаний, языков запросов,
возможность гибкой адаптации к изменениям в предметной области.
Простота и логическая природа языковых инструментов позволяет
организовать органичное взаимодействие с реляционными базами
данных, в частности, с SQL-ориентированными и дедуктивными
БД. Это свойство предоставляет дополнительные возможности
использования в логической среде информации из сетевых ресурсов. С
другой стороны, погружение в подобную среду может обеспечить более
мощные возможности для поддержки и оценки непротиворечивости
данных, чем в традиционных технологиях БД.
Часть предлагаемых средств использовалась для создания тренажеров,
обучающих проведению стыковки космических объектов. Возможность
динамического изменения спецификаций определила удобный способ
задания аварийных ситуаций и отработки реакции при неправильной
подаче или приеме сигналов, а также позволила обнаружить ошибки в
проектах программ, реализующих процесс стыковки. Метод и класс
спецификаций апробировались также для разработки языковых
процессоров и технологии генерации сетевых приложений из
объектно-ориентированной базы-заготовки.
Подход. Использование подхода предполагает выполнение двух
этапов. На первом этапе составляется описание исследуемого объекта
в предлагаемом логическом языке. В описание включаются: перечень
элементов, их атрибутов, отношений между ними, правила, индуктивно
определяющие эти отношения и атрибуты (зависимости между
элементами) и правила, задающие ограничения на зависимости --
условия "правильности" функционирования, аварийные ситуации и
т.п. В целом, правила должны полностью определять требуемые
свойства объекта и/или его поведение. Если необходима поддержка
корректности трансформаций исследуемой системы, то аналогичным
образом могут быть описаны и трансформационные преобразования. На
втором этапе подключаются интерпретаторы спецификаций, цель
которых -- построение логической модели объекта и проверка
выполнимости требуемых свойств. В процессе интерпретации
диагностируются кроме того логические ошибки -- противоречивость
и неполнота представления объекта или проекта системы.
Языковые средства. Описание -- спецификацию
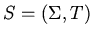 исследуемого объекта составляют сигнатура
исследуемого объекта составляют сигнатура 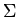 и теория
и теория
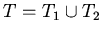 -- множество аксиом, определяющих
объект (
-- множество аксиом, определяющих
объект (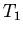 ) и ограничивающих его состояние или поведение
(
) и ограничивающих его состояние или поведение
(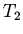 ).
На практике более адекватен многосортный логический язык, но для
простоты изложения далее используется односортная сигнатура.
Формально,
).
На практике более адекватен многосортный логический язык, но для
простоты изложения далее используется односортная сигнатура.
Формально,
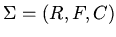 , где
, где 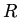 -- множество имен предикатов
(отношений),
-- множество имен предикатов
(отношений), 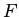 -- функций (атрибутов) и
-- функций (атрибутов) и 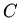 -- констант,
причем С не пусто и все константы различны. Отношение равенства
считается встроенным (аксиомы равенства автоматически добавляются
к
-- констант,
причем С не пусто и все константы различны. Отношение равенства
считается встроенным (аксиомы равенства автоматически добавляются
к 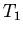 ). Константы кодируют элементы объекта (например,
конструкции программ или технические узлы, устройства, модули и
т.п.).
Обозначения:
). Константы кодируют элементы объекта (например,
конструкции программ или технические узлы, устройства, модули и
т.п.).
Обозначения: 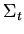 -- множество замкнутых термов
сигнатуры
-- множество замкнутых термов
сигнатуры 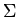 ,
, 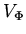 -- множество переменных формулы
-- множество переменных формулы
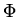 ; для произвольного множества
; для произвольного множества 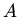 :
: 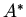 -- совокупность
конечных списков над
-- совокупность
конечных списков над 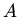 ,
, 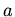 -- элемент
-- элемент 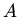 ,
,
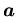 -- вектор
таких элементов; для всякой алгебраической системы
-- вектор
таких элементов; для всякой алгебраической системы 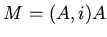 обозначает носитель,
обозначает носитель, 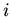 -- интерпретирующее отображение на
-- интерпретирующее отображение на 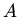 .
Аксиомы
.
Аксиомы 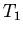 рассматриваются как индуктивные определения
объявленных в
рассматриваются как индуктивные определения
объявленных в 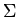 функций и отношений формулами вида
функций и отношений формулами вида
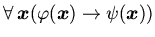 или или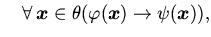 |
(1) |
где
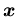 -- вектор переменных,
-- вектор переменных,
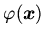 -- конъюнкция
атомарных формул вида
-- конъюнкция
атомарных формул вида
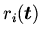 ,
,
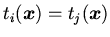 или их отрицаний (
или их отрицаний (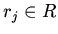 ,
,
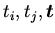 -- термы сигнатуры
-- термы сигнатуры
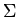 );
);
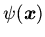 -- конъюнкция атомарных формул вида
-- конъюнкция атомарных формул вида
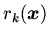 (определение отношения
(определение отношения 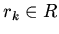 ) или
) или
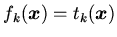 (определение функции
(определение функции 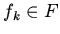 ).
). 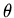 --
конечный список. При каждом отношении с отрицанием
--
конечный список. При каждом отношении с отрицанием
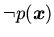 ,
содержащемся в
,
содержащемся в
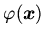 , должен присутствовать конъюнкт
, должен присутствовать конъюнкт
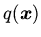 , позитивно входящий в эту же формулу, такой, что
, позитивно входящий в эту же формулу, такой, что
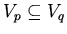 (т.о.
(т.о.
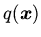 играет роль ограниченного квантора для
играет роль ограниченного квантора для
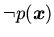 ).
Подкласс аксиом
).
Подкласс аксиом 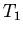 образуют формулы без переменных:
образуют формулы без переменных:
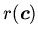 ,
,
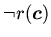 ,
,
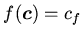 , составляющие множество фактов
, составляющие множество фактов 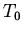 -- конкретных утверждений об объекте.
Ограничения
-- конкретных утверждений об объекте.
Ограничения 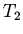 задаются произвольными формулами первого порядка
с ограниченными кванторами.
Для спецификаций определено понятие корректности, включающее в
себя свойства полноты определения функций, непротиворечивости
относительно аксиом равенства и непротиворечивости относительно
использования отрицаний.
Более точно, спецификация
задаются произвольными формулами первого порядка
с ограниченными кванторами.
Для спецификаций определено понятие корректности, включающее в
себя свойства полноты определения функций, непротиворечивости
относительно аксиом равенства и непротиворечивости относительно
использования отрицаний.
Более точно, спецификация
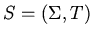 называется корректной,
если она:
называется корректной,
если она:
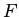 -полна:
-полна:
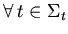
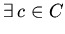 :
: 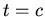 --
логическое следствие
--
логическое следствие 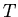 и
и 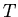 -- ациклична;
-- ациклична;
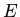 -непротиворечива:
-непротиворечива:
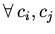 ,
, 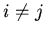 ,
, 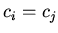 не
является следствием
не
является следствием 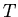 ;
;
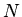 -непротиворечива:
-непротиворечива:
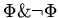 не является следствием
не является следствием 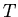 для всякой атомарной формулы
для всякой атомарной формулы 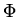 .
Требование ацикличности совокупности индуктивных определений
гарантирует для каждой
.
Требование ацикличности совокупности индуктивных определений
гарантирует для каждой
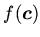 существование хотя бы одного
индуктивного доказательства
существование хотя бы одного
индуктивного доказательства
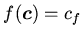 , свободного от вхождений
терма
, свободного от вхождений
терма
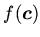 , т.е. исключает теории, редуцируемые к
определениям вида
, т.е. исключает теории, редуцируемые к
определениям вида
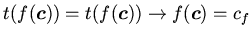 .
Ацикличность дает возможность интерпретатору, реализующему вывод,
не прибегая к дорогостоящему механизму унификации термов, получить
значение определяемых функций за конечное число шагов, индуктивно
вычисляя определяющие эти функции термы. Формально это свойство
моделируется выводимостью в теории
.
Ацикличность дает возможность интерпретатору, реализующему вывод,
не прибегая к дорогостоящему механизму унификации термов, получить
значение определяемых функций за конечное число шагов, индуктивно
вычисляя определяющие эти функции термы. Формально это свойство
моделируется выводимостью в теории 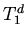 , полученной по
, полученной по 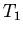 добавлением формул со специальным предикатом Def,
контролирующим определенность термов [3].
Понятие
добавлением формул со специальным предикатом Def,
контролирующим определенность термов [3].
Понятие 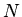 -непротиворечивости для теории
-непротиворечивости для теории 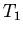 отличается от
обычной логической непротиворечивости, поскольку отрицания
используются лишь в посылках
отличается от
обычной логической непротиворечивости, поскольку отрицания
используются лишь в посылках
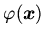 импликаций, и
сводится к непротиворечивости теорий
импликаций, и
сводится к непротиворечивости теорий
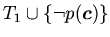 , в
которой отношения
, в
которой отношения
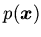 входят с отрицанием в формулы
входят с отрицанием в формулы
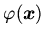 . Фактически это означает, что ни одна замкнутая
атомарная формула
. Фактически это означает, что ни одна замкнутая
атомарная формула
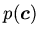 не может быть выведена как следствие
предположения об истинности
не может быть выведена как следствие
предположения об истинности
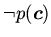 .
Семантика. Для обеспечения эффективной диагностики
логических ошибок предлагается использовать в качестве семантики
рассматриваемого класса спецификаций инициальные
индуктивно-вычислимые (ИВ-) модели из констант
.
Семантика. Для обеспечения эффективной диагностики
логических ошибок предлагается использовать в качестве семантики
рассматриваемого класса спецификаций инициальные
индуктивно-вычислимые (ИВ-) модели из констант 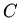 . Модель такого
типа строится по спецификации с помощью прямого вывода, в котором
используются только подстановки констант вместо переменных.
Поскольку тотальность функций требует существования следствий вида
. Модель такого
типа строится по спецификации с помощью прямого вывода, в котором
используются только подстановки констант вместо переменных.
Поскольку тотальность функций требует существования следствий вида
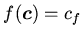 для каждой
для каждой 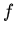 , вывод по определениям
, вывод по определениям 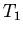 должен
давать однозначное вычисление всех
должен
давать однозначное вычисление всех 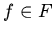 . Единственность
построения модели обеспечивает свойство инициальности, однако
способ получения инициальных моделей
. Единственность
построения модели обеспечивает свойство инициальности, однако
способ получения инициальных моделей 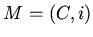 сам по себе не
гарантирует вычислимости интерпретирующей функции
сам по себе не
гарантирует вычислимости интерпретирующей функции 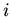 . Поэтому
выделен вычислимый подкласс таких моделей, семантически
эквивалентных множеству синтаксически "хорошо определенных",
т.е. корректных, спецификаций.
Свойство индуктивной вычислимости фактически обеспечивает
существование фундированного порядка на модели, при котором термы
условия определения могут быть вычислены прежде определяемых
значений и, таким образом, интерпретирующее отображение
. Поэтому
выделен вычислимый подкласс таких моделей, семантически
эквивалентных множеству синтаксически "хорошо определенных",
т.е. корректных, спецификаций.
Свойство индуктивной вычислимости фактически обеспечивает
существование фундированного порядка на модели, при котором термы
условия определения могут быть вычислены прежде определяемых
значений и, таким образом, интерпретирующее отображение 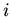 может
быть индуктивно вычислено по системе определений.
Доказано [3], что такая модель однозначно соответствует корректной
спецификации:
Спецификация
может
быть индуктивно вычислено по системе определений.
Доказано [3], что такая модель однозначно соответствует корректной
спецификации:
Спецификация
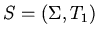 имеет инициальную
индуктивно-вычислимую модель
имеет инициальную
индуктивно-вычислимую модель
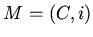 из констант
из констант 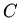 тогда и только тогда, когда
тогда и только тогда, когда 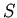 корректна.
Модель
корректна.
Модель 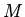 может быть построена в соответствии с общим алгоритмом
получения инициальных систем для квазитождеств [4]. В данном
случае, поскольку носитель модели -- множество
может быть построена в соответствии с общим алгоритмом
получения инициальных систем для квазитождеств [4]. В данном
случае, поскольку носитель модели -- множество 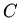 и все
константы различны, процесс порождения логических следствий теории
и все
константы различны, процесс порождения логических следствий теории
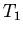 вида
вида
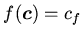 и
и
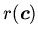 фактически означает
интерпретацию функций
фактически означает
интерпретацию функций 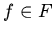 и отношений
и отношений 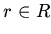 на
на 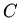 . Для
аксиом без отрицаний множество следствий образуется в результате
обычного логического вывода. Атомарные замкнутые следствия всей
теории можно получить, если задать интерпретацию для отношений
. Для
аксиом без отрицаний множество следствий образуется в результате
обычного логического вывода. Атомарные замкнутые следствия всей
теории можно получить, если задать интерпретацию для отношений
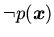 , входящих в
, входящих в 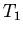 с отрицанием. Это означает попытку
построения максимально непротиворечивого (
с отрицанием. Это означает попытку
построения максимально непротиворечивого (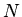 -) расширения теории
-) расширения теории
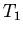 формулами вида
формулами вида
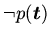 ,
,
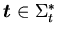 . Чтобы
выявить возможность существования инициальной модели у таких
спецификаций, необходимо принимать во внимание только строгие
. Чтобы
выявить возможность существования инициальной модели у таких
спецификаций, необходимо принимать во внимание только строгие
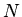 -расширения, в которых для всякого замкнутого следствия
-расширения, в которых для всякого замкнутого следствия
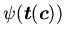 должно существовать определение, его
"породившее", с истинной посылкой
должно существовать определение, его
"породившее", с истинной посылкой
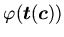 . Для
произвольной спецификации вида (1) таких расширений может быть
несколько. Доказано, что обладание инициальной строгой моделью для
теории
. Для
произвольной спецификации вида (1) таких расширений может быть
несколько. Доказано, что обладание инициальной строгой моделью для
теории 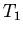 равносильно существованию единственного строгого
равносильно существованию единственного строгого
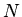 -расширения:
Спецификация
-расширения:
Спецификация
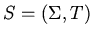 имеет индуктивно-вычислимую
инициальную строгую модель из констант тогда и только тогда, когда
имеет индуктивно-вычислимую
инициальную строгую модель из констант тогда и только тогда, когда
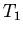 имеет единственное
имеет единственное 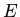 -непротиворечивое и
-непротиворечивое и 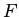 -полное
строгое
-полное
строгое 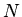 -расширение.
Конструктивная проверка существования такого расширения и
соответственно, процесс получения ИВ-модели сводится к построению
множества стратегий интерпретации, каждая из которых однозначно
соответствует некоторому отображению
-расширение.
Конструктивная проверка существования такого расширения и
соответственно, процесс получения ИВ-модели сводится к построению
множества стратегий интерпретации, каждая из которых однозначно
соответствует некоторому отображению 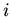 и строгому
и строгому
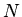 -расширению, и проверке эквивалентности этих стратегий.
Стратегия -- это фиксированная последовательность
-расширению, и проверке эквивалентности этих стратегий.
Стратегия -- это фиксированная последовательность 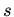 :
:
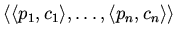 выбора аксиом и конъюнктов, содержащих
негативное вхождение предикатов
выбора аксиом и конъюнктов, содержащих
негативное вхождение предикатов 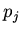 . Элемент
. Элемент
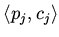 входит в стратегию
входит в стратегию 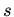 , если на некотором шаге вывода
неопределенный до этого на подстановке
, если на некотором шаге вывода
неопределенный до этого на подстановке
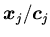 предикат
предикат
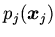 , был интерпретирован как ложный. Стратегия является
непротиворечивой, если пересечение областей истинности и ложности
всякого содержащегося в ней предиката
, был интерпретирован как ложный. Стратегия является
непротиворечивой, если пересечение областей истинности и ложности
всякого содержащегося в ней предиката 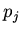 пусто
(непротиворечивость базы данных). Это означает, что множество
атомарных следствий теории
пусто
(непротиворечивость базы данных). Это означает, что множество
атомарных следствий теории 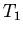 , полученное интерпретацией
, полученное интерпретацией 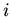 при стратегии
при стратегии 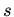 , образует
, образует 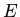 - и
- и 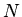 -непротиворечивую
элементарную теорию. Стратегия
-непротиворечивую
элементарную теорию. Стратегия 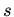 называется полной, если
соответствующее множество следствий образует
называется полной, если
соответствующее множество следствий образует 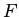 -полную теорию.
Стратегии
-полную теорию.
Стратегии 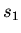 ,
, 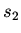 являются эквивалентными, если множества их
элементов совпадают. Доказано, что
Спецификация
являются эквивалентными, если множества их
элементов совпадают. Доказано, что
Спецификация 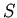 обладает инициальной ИВ-моделью
обладает инициальной ИВ-моделью 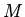 тогда и
только тогда, когда все непротиворечивые полные стратегии
эквивалентны.
Этот факт обосновывает анализ непротиворечивости спецификаций с
отрицаниями. Ценность этого критерия в том, что гарантируется
корректное построение минимальной модели, не требующее ограничений
рекурсии в определениях и введения какого-либо упорядочивания или
иерархии на множестве аксиом в
тогда и
только тогда, когда все непротиворечивые полные стратегии
эквивалентны.
Этот факт обосновывает анализ непротиворечивости спецификаций с
отрицаниями. Ценность этого критерия в том, что гарантируется
корректное построение минимальной модели, не требующее ограничений
рекурсии в определениях и введения какого-либо упорядочивания или
иерархии на множестве аксиом в 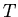 , как, например, процедуры
стратификации для обеспечения корректности обновлений в
реляционных [6] или дедуктивных базах данных. Однако реализация
этого критерия для конечных
, как, например, процедуры
стратификации для обеспечения корректности обновлений в
реляционных [6] или дедуктивных базах данных. Однако реализация
этого критерия для конечных 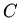 в общем случае имеет
экспоненциальную сложность. Условия понижения сложности
интерпретации до полиномов низких степеней сводятся к критериям
разрешимости проблемы существования модели с помощью единственной
стратегии и к выделению ограничений, сокращающих перебор
подстановок при определении истинности посылок (поскольку сам
вывод линеен).
Определен собственный подкласс индуктивно-вычислимых моделей,
минимальная относительно гомоморфного вложения система в котором
является инициальной в исходном классе. Такая модель может быть
построена с помощью единственной стратегии и однозначно
характеризует спецификацию с "хорошо определенной" рекурсией.
Это свойство разрешимо со сложностью не более, чем
в общем случае имеет
экспоненциальную сложность. Условия понижения сложности
интерпретации до полиномов низких степеней сводятся к критериям
разрешимости проблемы существования модели с помощью единственной
стратегии и к выделению ограничений, сокращающих перебор
подстановок при определении истинности посылок (поскольку сам
вывод линеен).
Определен собственный подкласс индуктивно-вычислимых моделей,
минимальная относительно гомоморфного вложения система в котором
является инициальной в исходном классе. Такая модель может быть
построена с помощью единственной стратегии и однозначно
характеризует спецификацию с "хорошо определенной" рекурсией.
Это свойство разрешимо со сложностью не более, чем 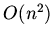 относительно символьной длины теории и проверяется статически, без
проведения интерпретации. Оно является более слабым ограничением,
чем принятые в логических языках, допускающих отрицания, и
запрещает только некоторые типы рекурсивной зависимости между
отношениями, входящими с отрицанием в предложения
относительно символьной длины теории и проверяется статически, без
проведения интерпретации. Оно является более слабым ограничением,
чем принятые в логических языках, допускающих отрицания, и
запрещает только некоторые типы рекурсивной зависимости между
отношениями, входящими с отрицанием в предложения 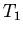 .
Интерпретатор. Для обеспечения точности диагностики
логических ошибок в качестве областей данных, на которых строится
функция
.
Интерпретатор. Для обеспечения точности диагностики
логических ошибок в качестве областей данных, на которых строится
функция 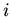 , рассматриваются полные решетки с низом --
"неопределенность" (
, рассматриваются полные решетки с низом --
"неопределенность" (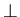 ), верхом -- "ошибка
переопределения" (
), верхом -- "ошибка
переопределения" (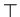 ) и отношением аппроксимации
) и отношением аппроксимации 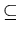 :
для любого элемента
:
для любого элемента 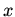 области
области 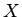 имеет место:
имеет место:
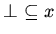 ,
,
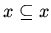 ,
,
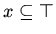 . Область значений истинности
представляет
. Область значений истинности
представляет
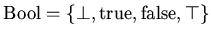 . Логические
операции -- конъюнкция, дизъюнкция, отрицание, а также равенство
монотонно доопределяются на области
. Логические
операции -- конъюнкция, дизъюнкция, отрицание, а также равенство
монотонно доопределяются на области
 . Используются также
монотонные "if... then... else" [5] и функция
. Используются также
монотонные "if... then... else" [5] и функция
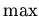 , определенная на списках и равная максимальному по
, определенная на списках и равная максимальному по
 элементу списка, причем
элементу списка, причем
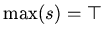 , если
, если 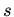 содержит
содержит 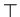 либо неравные элементы, т.е.
либо неравные элементы, т.е.
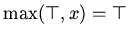 ;
;
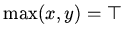 , если
, если 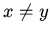 .
Интерпретатор вычисляет функцию
.
Интерпретатор вычисляет функцию 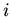 модели в соответствии с
денотационными уравнениями [3], задающими отображение сигнатурных
символов на множество функций и отношений на
модели в соответствии с
денотационными уравнениями [3], задающими отображение сигнатурных
символов на множество функций и отношений на 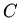 . Интерпретация
. Интерпретация
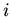 функций и формул на областях
функций и формул на областях
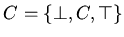 и
и
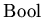 определяется индуктивно по структуре термов и формул. Для символов
сигнатуры
определяется индуктивно по структуре термов и формул. Для символов
сигнатуры 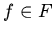 ,
, 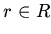 выбирается максимальный по
выбирается максимальный по
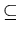 элемент по всем определениям
элемент по всем определениям 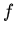 и
и 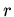 в
в 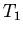 и всем
подстановкам
и всем
подстановкам 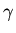 :
:
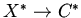 в этих определениях.
Монотонность дает возможность в случае возникновения ошибки
переопределения доопределить на значение
в этих определениях.
Монотонность дает возможность в случае возникновения ошибки
переопределения доопределить на значение 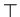 те функции и
отношения, вычисление которых было "задето" ошибкой. Так
фиксируется полный след ошибки и достигается однозначность
результата интерпретации.
Входом интерпретатора является исходное множество фактов, выходом
-- диаграмма модели
те функции и
отношения, вычисление которых было "задето" ошибкой. Так
фиксируется полный след ошибки и достигается однозначность
результата интерпретации.
Входом интерпретатора является исходное множество фактов, выходом
-- диаграмма модели 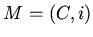 -- множество замкнутых атомарных
следствий теории
-- множество замкнутых атомарных
следствий теории 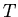 . На полученной модели, если она существует,
проверяются аксиомы
. На полученной модели, если она существует,
проверяются аксиомы 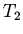 .
Алгоритм интерпретации состоит в поочередном выполнении двух шагов
до тех пор, пока не будет получена неподвижная точка вычислений.
На первом шаге интерпретируются определения, не содержащие
отрицаний. Каждый полученный новый факт -- следствие инициирует
выполнение правила, содержащего в посылке вхождение
соответствующего отношения или функции. Ищется подходящая
подстановка констант и определяется истинность левой части
правила. Если значение интерпретации этой формулы -- истина или
.
Алгоритм интерпретации состоит в поочередном выполнении двух шагов
до тех пор, пока не будет получена неподвижная точка вычислений.
На первом шаге интерпретируются определения, не содержащие
отрицаний. Каждый полученный новый факт -- следствие инициирует
выполнение правила, содержащего в посылке вхождение
соответствующего отношения или функции. Ищется подходящая
подстановка констант и определяется истинность левой части
правила. Если значение интерпретации этой формулы -- истина или
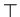 , то определяемые в правой части отношения и функции на этой
подстановке интерпретируются как истинные или равные
, то определяемые в правой части отношения и функции на этой
подстановке интерпретируются как истинные или равные 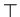 соответственно. Полученные таким образом факты, если они являются
новыми, продолжают активизировать действия шага 1. Если новых
фактов нет (локальная неподвижная точка), начинается выполнение
шага 2 -- интерпретация негативно входящих отношений, в
соответствии с семантикой спецификаций с отрицанием. Новые факты
соответственно. Полученные таким образом факты, если они являются
новыми, продолжают активизировать действия шага 1. Если новых
фактов нет (локальная неподвижная точка), начинается выполнение
шага 2 -- интерпретация негативно входящих отношений, в
соответствии с семантикой спецификаций с отрицанием. Новые факты
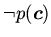 (если они есть) инициируют выполнение определений с
отрицаниями и повторение шага 1, если получены новые следствия.
Доказано, что интерпретатор строит модель, если она существует, не
зацикливается и завершает работу за конечное число шагов.
Емкостная сложность интерпретации имеет порядок
(если они есть) инициируют выполнение определений с
отрицаниями и повторение шага 1, если получены новые следствия.
Доказано, что интерпретатор строит модель, если она существует, не
зацикливается и завершает работу за конечное число шагов.
Емкостная сложность интерпретации имеет порядок 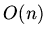 , где
, где 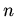 -
мощность модели, временная оценивается произведением
-
мощность модели, временная оценивается произведением 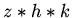 , где
, где
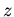 -- сложность нахождения подходящих подстановок для одной
аксиомы,
-- сложность нахождения подходящих подстановок для одной
аксиомы, 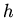 -- количество обращений к интерпретации аксиомы,
-- количество обращений к интерпретации аксиомы, 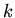 -- количество аксиом. Поскольку интерпретация предложений
активизируется только получением нового факта, величина
-- количество аксиом. Поскольку интерпретация предложений
активизируется только получением нового факта, величина 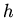 не
превышает
не
превышает 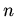 . Значение
. Значение 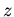 определяется как сложностью алгоритмов
поиска подстановок в базе данных, так и видом зависимости
переменных в условиях
определяется как сложностью алгоритмов
поиска подстановок в базе данных, так и видом зависимости
переменных в условиях
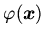 (типом графа, в котором
отношения
(типом графа, в котором
отношения 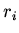 -- дуги, а переменные
-- дуги, а переменные 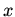 -- узлы). Если,
например, граф зависимости представляет собой пучок или множество
параллельных дуг, то
-- узлы). Если,
например, граф зависимости представляет собой пучок или множество
параллельных дуг, то 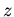 имеет порядок
имеет порядок 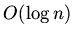 .
Модули. Концепция и средства модульной логической
спецификации основаны на идеях и методе параметризации и
элементарной определимости моделей, изложенных в [2]. Пусть
.
Модули. Концепция и средства модульной логической
спецификации основаны на идеях и методе параметризации и
элементарной определимости моделей, изложенных в [2]. Пусть
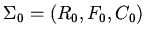 -- некоторая базовая сигнатура,
-- некоторая базовая сигнатура,
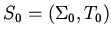 -- спецификация,
-- спецификация,
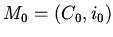 --
ИВ-модель спецификации
--
ИВ-модель спецификации 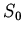 . Применяя используемый класс
спецификаций в качестве порождающего механизма для получения
ИВ-моделей, можно задать иерархию моделей, используя на первом
шаге
. Применяя используемый класс
спецификаций в качестве порождающего механизма для получения
ИВ-моделей, можно задать иерархию моделей, используя на первом
шаге 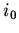 как начальный вход для интерпретации рекурсивных
определений некоторой спецификации
как начальный вход для интерпретации рекурсивных
определений некоторой спецификации 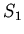 , затем полученную модель
, затем полученную модель
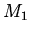 как базовую для следующей итерации
как базовую для следующей итерации 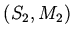 и т.д.
Поскольку модели определяются вычислимыми спецификациями,
процедура построения "модели моделей" конструктивна и позволяет
обосновать процесс последовательного уточнения модулей.
Пусть
и т.д.
Поскольку модели определяются вычислимыми спецификациями,
процедура построения "модели моделей" конструктивна и позволяет
обосновать процесс последовательного уточнения модулей.
Пусть
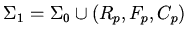 -- обогащение
-- обогащение
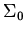 , полученное добавлением предикатных (
, полученное добавлением предикатных (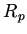 ),
функциональных (
),
функциональных (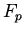 ), константных (
), константных (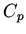 ) переменных.
Параметрическая спецификация (схема)
) переменных.
Параметрическая спецификация (схема)
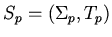 включает
в качестве определяемых в
включает
в качестве определяемых в 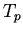 отношений и функций переменные
(параметры) из
отношений и функций переменные
(параметры) из 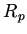 и
и 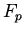 ; другие
; другие 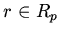 ,
, 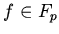 ,
входящие в
,
входящие в 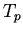 , рассматриваются как параметры со встроенной
интерпретацией (внешние). Пусть
, рассматриваются как параметры со встроенной
интерпретацией (внешние). Пусть 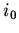 -- базовая интерпретация
-- базовая интерпретация
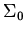 ,
, 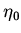 -- некоторая интерпретация внешних
параметров,
-- некоторая интерпретация внешних
параметров,
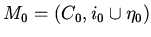 ,
, 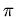 -- оператор,
сопоставляющий при каждом означивании параметров
-- оператор,
сопоставляющий при каждом означивании параметров 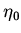 набору
отношений и функций
набору
отношений и функций 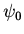 из
из 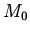 набор
набор
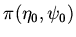 ,
определяемый как:
,
определяемый как:
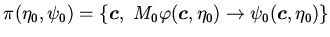 , где
, где
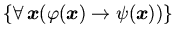 входят в
входят в 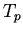 .
Индуктивное определение:
.
Индуктивное определение:
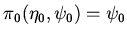 ;
;
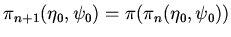 . Имеет место:
Для каждых
. Имеет место:
Для каждых 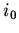 ,
, 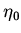 и параметрической спецификации
и параметрической спецификации 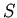 оператор
оператор 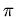 имеет неподвижную точку
имеет неподвижную точку
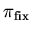 ,
являющуюся объединением
,
являющуюся объединением
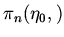 ,
, 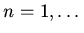 Теорема является следствием аналогичного результата для
Теорема является следствием аналогичного результата для
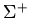 -программ [2].
Доопределим
-программ [2].
Доопределим 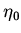 до
до 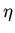 , поставив в соответствие
определяемым параметрам из
, поставив в соответствие
определяемым параметрам из 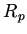 ,
, 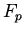 набор
набор
 .
Пара
.
Пара
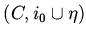 является моделью параметрической
спецификации
является моделью параметрической
спецификации 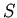 . Семантику
. Семантику 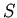 задает класс инициальных
ИВ-моделей.
В приведенной схеме в качестве input- и output-параметров могут
выступать функции и отношения. Передача в качестве фактического
параметра встроенной или уже полученной интерпретации -- аналог
вызова-по-значению в процедурных языках -- означает передачу
уже готового элемента модели, который не может быть доопределен.
Передача параметра-модуля -- аналог вызова-по-имени -- означает
передачу спецификации, которая может участвовать в порождении
новой модели -- экземпляра схемы.
Поскольку схема -- параметрическая спецификация представляет
класс моделей, то точную диагностику ошибок можно провести только
при интерпретации спецификации с конкретизированными параметрами.
Однако, предварительная (статическая) диагностика может быть
проведена интерпретацией схемы, где в качестве сигнатуры
используются имена формальных параметров, а в качестве входа --
множество (параметризованных) фактов или пустое множество.
При представлении трансформаций схема может быть частично
параметризована и соответствующая модель -- "частично
построена" (аналог смешанных вычислений). Диагностика такой
спецификации также будет неполной, где неопределенность функции
(не получение ею значения-константы) либо не считается ошибкой,
либо снимается доопределением функции на значение невычисленного
терма (т.е. константу представляет терм, символ которого
включается во множество
задает класс инициальных
ИВ-моделей.
В приведенной схеме в качестве input- и output-параметров могут
выступать функции и отношения. Передача в качестве фактического
параметра встроенной или уже полученной интерпретации -- аналог
вызова-по-значению в процедурных языках -- означает передачу
уже готового элемента модели, который не может быть доопределен.
Передача параметра-модуля -- аналог вызова-по-имени -- означает
передачу спецификации, которая может участвовать в порождении
новой модели -- экземпляра схемы.
Поскольку схема -- параметрическая спецификация представляет
класс моделей, то точную диагностику ошибок можно провести только
при интерпретации спецификации с конкретизированными параметрами.
Однако, предварительная (статическая) диагностика может быть
проведена интерпретацией схемы, где в качестве сигнатуры
используются имена формальных параметров, а в качестве входа --
множество (параметризованных) фактов или пустое множество.
При представлении трансформаций схема может быть частично
параметризована и соответствующая модель -- "частично
построена" (аналог смешанных вычислений). Диагностика такой
спецификации также будет неполной, где неопределенность функции
(не получение ею значения-константы) либо не считается ошибкой,
либо снимается доопределением функции на значение невычисленного
терма (т.е. константу представляет терм, символ которого
включается во множество 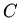 ).
В качестве модуля может выступать параметрическое определение
отношения или функции, а также параметрическая спецификация
(схема), используемая, например, как генератор типов.
Соответственно параметром может быть модель (множество исходных
фактов), множество констант, спецификация (определение конкретного
отношения или функции), параметрическая спецификация (модуль).
Анализ соответствия фактических и формальных параметров,
идентификация переменных выполняются в рамках этого же подхода:
аксиоматизируются правила "видимости" переменных и соответствия
типов, контекстные условия и запускается интерпретатор, который в
данном случае играет роль семантического анализатора, как это было
сделано для языков программирования [1].
Трансформации и модификации. Преобразования моделируемого
объекта сводятся к изменениям его логической модели (и,
соответственно, спецификаций) которые можно представить
комбинацией следующих базовых трансформаций:
1. Доопределение функций и отношений на исходном множестве
).
В качестве модуля может выступать параметрическое определение
отношения или функции, а также параметрическая спецификация
(схема), используемая, например, как генератор типов.
Соответственно параметром может быть модель (множество исходных
фактов), множество констант, спецификация (определение конкретного
отношения или функции), параметрическая спецификация (модуль).
Анализ соответствия фактических и формальных параметров,
идентификация переменных выполняются в рамках этого же подхода:
аксиоматизируются правила "видимости" переменных и соответствия
типов, контекстные условия и запускается интерпретатор, который в
данном случае играет роль семантического анализатора, как это было
сделано для языков программирования [1].
Трансформации и модификации. Преобразования моделируемого
объекта сводятся к изменениям его логической модели (и,
соответственно, спецификаций) которые можно представить
комбинацией следующих базовых трансформаций:
1. Доопределение функций и отношений на исходном множестве
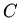 (задачи анализа). Пусть
(задачи анализа). Пусть
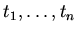 --
последовательность трансформаций, реализующая преобразование
объекта (программы, проекта, системы) из состояния
--
последовательность трансформаций, реализующая преобразование
объекта (программы, проекта, системы) из состояния 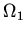 в
состояние
в
состояние 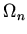 . В качестве логического представления
трансформации
. В качестве логического представления
трансформации 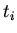 рассматривается спецификация
рассматривается спецификация
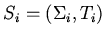 , а сам процесс трансформации состоит в
интерпретации
, а сам процесс трансформации состоит в
интерпретации 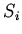 -- получении минимальной модели
-- получении минимальной модели
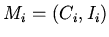 , представляющей семантику
, представляющей семантику 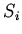 . Условием
корректности всякой трансформации
. Условием
корректности всякой трансформации 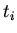 тогда является условие
правильности спецификации
тогда является условие
правильности спецификации 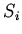 :
У1). Трансформация
:
У1). Трансформация 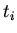 корректна тогда и только тогда,
когда
корректна тогда и только тогда,
когда 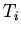 имеет модель
имеет модель 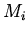 . Это условие эквивалентно
непротиворечивости (относительно равенства и использования
отрицаний) и
. Это условие эквивалентно
непротиворечивости (относительно равенства и использования
отрицаний) и 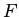 -полноте спецификации
-полноте спецификации 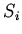 .
Условие У1 не ограничивает поведение последовательности
трансформаций. Корректность всего цикла преобразований может
потребовать выполнения дополнительных ограничений. Например, если
для всякого
.
Условие У1 не ограничивает поведение последовательности
трансформаций. Корректность всего цикла преобразований может
потребовать выполнения дополнительных ограничений. Например, если
для всякого 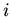
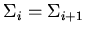 , то каждая
, то каждая 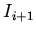 получена доопределением
получена доопределением 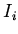 . Тогда имеем:
У2) Последовательность
. Тогда имеем:
У2) Последовательность
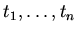 трансформаций
корректна, если корректна каждая
трансформаций
корректна, если корректна каждая 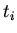 , и
, и
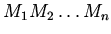 , где
, где
 -- отношение гомоморфного вложения.
Условие У2 является достаточно слабым для последовательности
трансформаций. В частности, оно не требует корректности совокупной
спецификации
-- отношение гомоморфного вложения.
Условие У2 является достаточно слабым для последовательности
трансформаций. В частности, оно не требует корректности совокупной
спецификации
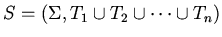 . Поскольку
допускаются формулы с отрицанием, и вывод с фактами, полученными
на шаге
. Поскольку
допускаются формулы с отрицанием, и вывод с фактами, полученными
на шаге 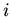 не повторяется для спецификаций
не повторяется для спецификаций 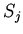 ,
, 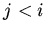 , то
минимальная модель
, то
минимальная модель 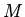 для
для 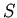 , хотя и может существовать, но не
обязательно является объединением моделей
, хотя и может существовать, но не
обязательно является объединением моделей 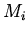 .
2. Добавление новых элементов, отношений и атрибутов
(пошаговое уточнение, задачи проектирования и синтеза). Если при
преобразованиях
.
2. Добавление новых элементов, отношений и атрибутов
(пошаговое уточнение, задачи проектирования и синтеза). Если при
преобразованиях
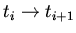 сигнатура расширяется, т.е.
сигнатура расширяется, т.е.
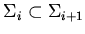 , то корректность последовательности
трансформаций поддерживает следующее условие:
У3) последовательность трансформаций
, то корректность последовательности
трансформаций поддерживает следующее условие:
У3) последовательность трансформаций
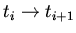 корректна, если корректна каждая из них и модель
корректна, если корректна каждая из них и модель 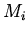 является
подсистемой
является
подсистемой 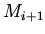 в сигнатуре
в сигнатуре
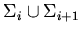 , причем
, причем
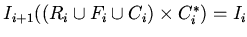 .
Символ
.
Символ
 обозначает операцию ограничения
функции.
3. Сужение исходной логической структуры (удаление
элементов, задачи оптимизации). Это немонотонное в общем случае
преобразование, тем не менее, в ряде задач может быть представлено
в рамках рассматриваемого класса спецификаций. В аксиомы
обозначает операцию ограничения
функции.
3. Сужение исходной логической структуры (удаление
элементов, задачи оптимизации). Это немонотонное в общем случае
преобразование, тем не менее, в ряде задач может быть представлено
в рамках рассматриваемого класса спецификаций. В аксиомы 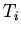 добавляется переменная времени или состояния, пробегающая конечный
интервал, например,
добавляется переменная времени или состояния, пробегающая конечный
интервал, например,
![$ H=[h_1,\dots,h_n]$](img161.gif) ,
, 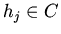 , "шагов":
, "шагов":
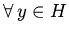 ,
,
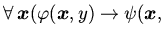 next
next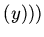 . Корректность трансформаций
. Корректность трансформаций 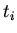 тогда определяется условием У1, а для их последовательности должно
выполняться:
тогда определяется условием У1, а для их последовательности должно
выполняться:
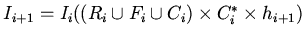 . При добавлении в вектор
аргументов переменной
. При добавлении в вектор
аргументов переменной 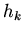 метятся все элементы отношений,
которые нужно "оставить". Это не всегда удобно, если работает
рекурсивное правило, например, транзитивного замыкания отношения
подчинения узлов на дереве. Заранее невозможно определить
требуемое количество шагов, и непросто поэтому задать
трансформацию, касающуюся последнего шага. В этих случаях удобнее
использовать отношение "удален", помечающее элементы, которые
можно "выбросить". Например, два следующих правила задают
необходимое преобразование
метятся все элементы отношений,
которые нужно "оставить". Это не всегда удобно, если работает
рекурсивное правило, например, транзитивного замыкания отношения
подчинения узлов на дереве. Заранее невозможно определить
требуемое количество шагов, и непросто поэтому задать
трансформацию, касающуюся последнего шага. В этих случаях удобнее
использовать отношение "удален", помечающее элементы, которые
можно "выбросить". Например, два следующих правила задают
необходимое преобразование 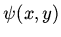 на последнем, уже
сохраняемом элементе отношения:
на последнем, уже
сохраняемом элементе отношения:
| |
|
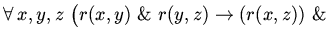 удален удален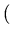 имя имя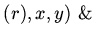 удален удален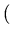 имя имя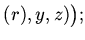 |
|
| |
|
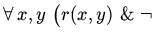 удален удален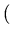 имя имя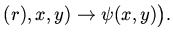 |
|
В некоторых работах для спецификации удаляемого элемента отношения
вводится отрицание в правую часть формулы:
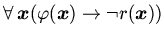 . Такой подход, однако, требует определения
нестандартной (нелогической) семантики отрицания, т.к.
использование обычной семантики немедленно приводит к противоречию
-- порождению и отрицанию элемента одновременно.
Если трансформации выполняются асинхронно или параллельно, или
проводится многоэтапная рекурсивная трансформация, то необходимым
условием корректности трансформаций является существование для
совокупной спецификации
. Такой подход, однако, требует определения
нестандартной (нелогической) семантики отрицания, т.к.
использование обычной семантики немедленно приводит к противоречию
-- порождению и отрицанию элемента одновременно.
Если трансформации выполняются асинхронно или параллельно, или
проводится многоэтапная рекурсивная трансформация, то необходимым
условием корректности трансформаций является существование для
совокупной спецификации 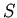 минимальной модели, изоморфной
объединению моделей
минимальной модели, изоморфной
объединению моделей 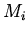 .
Условия корректности трансформаций связаны, как правило, не только
с проблемой "хорошей определенности" спецификаций трансформаций,
но и с предметной областью, с целями проводимых преобразований.
Сохранение некоторых требуемых свойств (инварианты трансформации)
может быть специфицировано явно, в виде аксиом-ограничений,
проверяемых на уже полученной модели -- результате трансформации,
или являться следствием условий корректности, налагаемых на
последовательность преобразований в целом. Так, например, если
преобразовывалась некоторая программа, то условие У2) гарантирует
сохранение ее семантической функции.
Динамические взаимодействия. Возможность представления
динамических свойств реализуется включением переменных времени в
логические формулы. Эти переменные пробегают конечные отрезки
.
Условия корректности трансформаций связаны, как правило, не только
с проблемой "хорошей определенности" спецификаций трансформаций,
но и с предметной областью, с целями проводимых преобразований.
Сохранение некоторых требуемых свойств (инварианты трансформации)
может быть специфицировано явно, в виде аксиом-ограничений,
проверяемых на уже полученной модели -- результате трансформации,
или являться следствием условий корректности, налагаемых на
последовательность преобразований в целом. Так, например, если
преобразовывалась некоторая программа, то условие У2) гарантирует
сохранение ее семантической функции.
Динамические взаимодействия. Возможность представления
динамических свойств реализуется включением переменных времени в
логические формулы. Эти переменные пробегают конечные отрезки 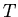 дискретного набора точек, каждая из которых может задаваться либо
конкретной датой, либо событием (именем или сигналом события).
Например, интерпретация предложения:
дискретного набора точек, каждая из которых может задаваться либо
конкретной датой, либо событием (именем или сигналом события).
Например, интерпретация предложения:
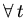 ,
, 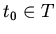 (
сигнал
(
сигнал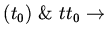 режим
режим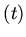 ) установит состояние режим для временных точек
интервала
) установит состояние режим для временных точек
интервала 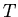 после момента
после момента 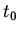 -- времени наступления события
сигнал. Такого рода спецификации использовались для
моделирования космических тренажеров, где время получения сигнала
и входа в требуемое состояние было точно задано.
Использование переменных времени позволяет обеспечить монотонность
вычислений при интерпретации трансформаций структуры объекта или
преобразовании модели, а также сохранять историю проекта в рамках
единой языковой и инструментальной среды.
Некоторые примеры спецификаций, использованных на практике, можно
найти в [3] (прототипирование процесса космической стыковки) и в
[1] (семантический анализ по спецификации статической семантики
языков Алгол и Модула-2). Несмотря на сложное математическое
обоснование, практические спецификации выглядят ясно и просто.
Например, все правила видимости переменных в языке Модула-2
составляют четыре аксиомы-определения и две аксиомы-ограничения,
описывающие контекстные условия.
-- времени наступления события
сигнал. Такого рода спецификации использовались для
моделирования космических тренажеров, где время получения сигнала
и входа в требуемое состояние было точно задано.
Использование переменных времени позволяет обеспечить монотонность
вычислений при интерпретации трансформаций структуры объекта или
преобразовании модели, а также сохранять историю проекта в рамках
единой языковой и инструментальной среды.
Некоторые примеры спецификаций, использованных на практике, можно
найти в [3] (прототипирование процесса космической стыковки) и в
[1] (семантический анализ по спецификации статической семантики
языков Алгол и Модула-2). Несмотря на сложное математическое
обоснование, практические спецификации выглядят ясно и просто.
Например, все правила видимости переменных в языке Модула-2
составляют четыре аксиомы-определения и две аксиомы-ограничения,
описывающие контекстные условия.
Литература
-
Глушкова В. Н., Ильичева О. А. К пpоблеме видимости и
типизации в языке МОДУЛА-2. Язык МОДУЛА-2, его pеализация и
использование. Сб. ВЦ СО РАH, Hовосибиpск, 1989.
-
Гончаров С. С., Свириденко Д. И.
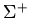 -программы и их
семантики. Вычислительные системы, 120, 1987, 24-51.
-программы и их
семантики. Вычислительные системы, 120, 1987, 24-51.
-
Ильичева О. А. Средства эффективной диагностики ошибок для
систем логического прототипирования. Автоматика и телемеханика,
9, 1997, 185-196.
-
Мальцев А. И. Алгебраические системы. Наука, Москва, 1970.
-
Манна З. Теория неподвижной точки программ. Кибернетический
сборник, 15. Мир, Москва, 1978, 38-100.
-
Louiqa Raschid, Jorge Lobo. Semantics for Update Rule
Programs and Implementation in a Relational Database Management
System. ACM Transaction on Database Systems, Vol.22, 4, 1996,
526-571.
© 2001, Сибирское отделение Российской академии наук, Новосибирск
© 2001, Объединенный институт информатики СО РАН, Новосибирск
© 2001, Институт вычислительных технологий СО РАН, Новосибирск
© 2001, Институт систем информатики СО РАН, Новосибирск
© 2001, Институт математики СО РАН, Новосибирск
© 2001, Институт цитологии и генетики СО РАН, Новосибирск
© 2001, Институт вычислительной математики и математической геофизики СО РАН, Новосибирск
© 2001, Новосибирский государственный университет
Дата последней модификации Thursday, 06-Sep-2001 14:19:12 NOVST

 Ваши комментарии
Ваши комментарии
![[SBRAS]](/gif/s_sigma.gif)