Моделирование регуляторных механизмов живых систем 1

Хидиров Б.Н.
Институт кибернетики, Ташкент

Аннотация:

Рассматривается один из возможных подходов к количественному исследованию механизмов регуляции живых систем. Уравнения состояния регуляторной системы построены с учетом кооперативности процессов, наличия комбинированной обратной связи и временных взаимоотношений в регуляционной цепи. Результаты качественного исследования уравнений состояния регуляторной системы и их модельных систем показывают существование решений в виде устойчивого стационарного состояния, периодических и нерегулярных колебаний. В некоторых случаях наблюдается эффект "черная дыра'' - срыв решений к тривиальному аттрактору. Применение результатов модельных исследований для анализа некоторых биологических задач показывает, как нам представляется, применимость предлагаемого метода при количественном исследовании механизмов регуляции живых систем в норме и при аномалиях.


One of the possible approaches for quantitative studies of regulatory mechanisms of living system is considered. The equations of system state are constructed taking into account the cooperation of processes, presence of combined feedback and temporary relations in regulation loop. Results of the qualitative analysis of an equations and their model systems shows existence of following functioning regimes: rest, stable functional state, periodic and irregular fluctuations. In some cases the effect "black hole'' - break-down of solutions to trivial attractor is observed. The results application of model investigations for the analysis some biological problems shows, according to our opinion, that the proposed method can be used for quantitative studies of living system mechanisms at norm and anomalies.

Введение

Развитие кибернетических подходов в исследовании живого  [3,4,7,8,9] привело к бурному росту количества научных работ по моделированию механизмов управления живых систем. Были созданы основы моделирования эволюции на ЭВМ, теория молекулярно-генетических систем управления, методы моделирования механизмов регуляции внутриклеточных процессов, клеточных функций и клеточных сообществ  [2,3,6,7,10,12,13].

Математические модели живых систем предназначены для количественного анализа поведения множества элементов (комплекса макромолекул), функционирующих в некоторой особой среде и способных реагировать на определенные внешние воздействия. Это приводит  [18,19] к формулировке понятий $or$ (операторов-регуляторов) - элементов регуляторной системы, способной к восприятию и выработке сигналов определенной природы, и $asta$ (active system with time average) - сигнальной среды регуляторной системы, в которой взаимосвязанная деятельность элементов осуществляется, на основе обратных связей, с некоторым средним временем h (временем, прошедшим с момента образования сигналов до момента воздействия их (или их продуктов) на активность элементов)  [18]. Комплекс $or$ вместе с $asta$ составляет регуляторную систему - $orasta$. Геометрия подобных регуляторных систем является динамической, в которой понятие неподвижной точки теряет смысл  [19]. Единицей времени $orasta$ является $h$. В природе наблюдаются случаи раздельного существования $or$ и $asta$. Примером $or$ без $asta$ являются вирусы, а $asta$ без $or$ - зрелые безъядерные эритроциты.

Основные уравнения

Пусть имеем $orasta$ с $n$ элементами. Уравнения активности $or$ данной регуляторной системы, построенные на основе обобщения подходов Б. Гудвина при моделировании механизмов регуляции внутриклеточных процессов  [6], В.А. Ратнера и М. Эйгена при моделировании механизмов эволюции макромолекул  [9,11,21], с учетом кооперативности рассматриваемых процессов, временных взаимоотношений и наличия комбинированной обратной связи в $asta$  [18,19], имеют вид
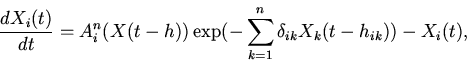\begin{displaymath} \frac{dX_{i}(t)}{dt}=A_{i}^{n}(X(t-h)) \exp({-\sum \limits_{k=1}^{n}\delta_{ik}X_{k}(t-h_{ik})}) - X_{i}(t), \end{displaymath} (1)

c

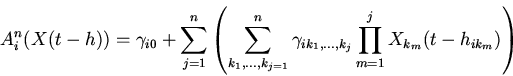
\begin{displaymath} A_{i}^{n}(X(t-h))=\gamma_{i0}+ \sum \limits_{j=1}^{n} \lef... ...}} \prod \limits _{m=1}^{j} X_{k_{m}}(t- h_{ik_{m}}) \right) \end{displaymath}

где $X_{i}(t)$ - величина, характеризующая количество сигнала, $i$-го $or$ в момент времени $t$; $h_{ik}$ - временное расстояние от $k$-го $or$ до $i$-го $or$ (в общем случае непрерывные функции); $h$ - максимальное среди $h_{ik}$;$\gamma_{i0}$ - параметры сигналообразования $asta$; $\gamma_{ik_{1},...,k_{j}}$, ${\delta_{ik}}$, $b_{i}$ - постоянные, $i_{k_{1},...k_{j}}$, $i,j, k_{j} = 1,2,...,n $. Вектор $M_{c}(C_{1},...,C_{n})$, значения элементов которого вычисляются по формулам
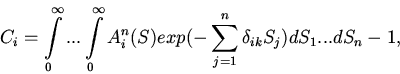\begin{displaymath} C_{i}=\int \limits_{0}^{\infty}...\int \limits_{0}^{\infty}... ...sum \limits_{j=1}^{n}\delta_{ik}S_{j}}) dS_{1}...dS_{n} - 1, \end{displaymath} (2)

называется "мерой эволюции регуляторной системы'' и определяет возможные варианты ее развития, так как его величина, в случае конкретных регуляторных систем, выделяет области их возможных поведений на параметрическом портрете (1). С другой стороны, $M_{с}$ выражает взаимоотношение регуляторной системы с внешней средой, поскольку его значение определяется заданными конкретными значениями коэффициентов (1)  [19]. В случае $M_{с} = 0$ система находится в "равновесии'' с внешней средой.

Уравнение (1) относится к классу функционально-дифференциальных уравнений и, при задании непрерывных функций на начальном временном отрезке длины $h$, ее непрерывное решение может быть получено методом последовательного интегрирования  [16]. При реализации данного метода на современных ЭВМ возникает задача построения решений по заданным дискретным значениям искомых переменных, которая является актуальной и при количественном описании биологических процессов функционально-дифференциальными уравнениями при наличии только дискретных экспериментальных данных. Данная задача для определенного класса линейных функционально- дифференциальных уравнений является разрешимой и разработанный метод построения их решений  [16] можно использовать при количественном анализе поведения решений (1).

Уравнения простейших регуляторных систем

Рассмотрим упрощенные (масштабированием, предположениями отсутствия сигналообразования в среде и наличия общего времени обратной связи - единицы времени orasta: $h_{ij}=h; i,j=1,2,...,n$) уравнения простейших (ассоциативных, взаимосопряженных и самосопряженных) регуляторных систем. В случае ассоциативных регуляторных систем для функционирования $i$-го $or$ необходима суммарная активность группы $or$. Имеем

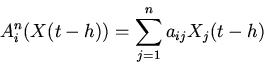
\begin{displaymath} A_{i}^{n}(X(t-h))= \sum \limits_{j=1}^{n}a_{ij}X_{j}(t-h) \end{displaymath}


\begin{displaymath} a_{ij} \geq 0 \qquad (i,j=1,2,...,n) \end{displaymath}

и для количественного исследования функционирования ассоциативных $orasta$ справедливы уравнения
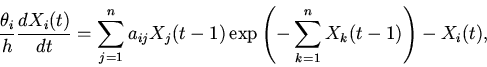\begin{displaymath} \frac{\theta_{i}}{h}\frac{dX_{i}(t)}{dt}= \sum \limits_{j=... ...exp\left(-\sum \limits_{k=1}^{n} X_{k}(t-1)\right)-X_{i}(t), \end{displaymath} (3)

где значения $\theta_{i}$, $a_{ij}$ $(i,j = 1,2,..,n)$ определяются посредством значений коэффициентов (1). Для элементов вектора $M_{c}$ имеем

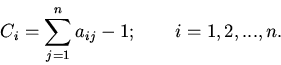
\begin{displaymath} C_{i}=\sum \limits_{j=1}^{n}a_{ij}-1; \qquad i = 1,2,...,n. \end{displaymath}

Функционирование взаимосопряженных регуляторных систем требует наличия продуктов всех $or$. Имеем
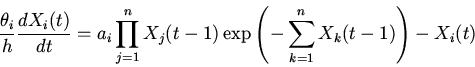\begin{displaymath} \frac{\theta_{i}}{h}\frac{dX_{i}(t)}{dt}= a_{i}\prod \limi... ...\exp\left(-\sum \limits_{k=1}^{n} X_{k}(t-1)\right)-X_{i}(t) \end{displaymath} (4)


\begin{displaymath} C_{i}=a_{i}-1; \qquad i=1,2,...,n. \end{displaymath}

В случае равновесия с внешней средой имеем $a_{i} = 1$ $(i=1,2,...,n)$. В некоторых случаях для функционирования $or$ регуляторной системы необходимо $n$ сигналов одного и того же $or$ ($n$ в данном случае можно ассоциировать с коэффициентом Хилла). Тогда функционирование всех $or$ происходит идентичным образом и
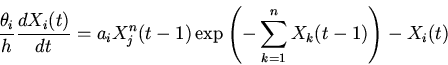\begin{displaymath} \frac{\theta_{i}}{h}\frac{dX_{i}(t)}{dt}= a_{i}X_{j}^{n}(t-1)\exp\left(-\sum \limits_{k=1}^{n} X_{k}(t-1)\right)-X_{i}(t) \end{displaymath} (5)


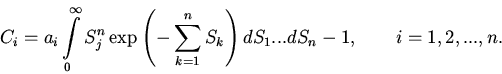
\begin{displaymath} C_{i}=a_{i}\int \limits_{0}^{\infty}S_{j}^{n}\exp\left(- \... ...k=1}^{n}S_{k}\right)dS_{1}...dS_{n}- 1, \qquad i = 1,2,...,n. \end{displaymath}

Здесь можно рассматривать предельный случай одного $or$. Тогда имеем самосопряженную регуляторную систему, функционирование которой описывается следующим уравнением
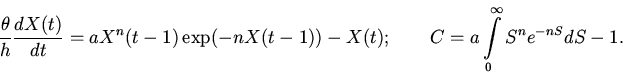\begin{displaymath} \frac{\theta}{h}\frac{dX(t)}{dt}= aX^{n}(t-1)\exp(-nX(t-1))-X(t); \qquad C=a\int \limits_{0}^{\infty}S^{n}e^{-nS}dS - 1. \end{displaymath} (6)

В случае равновесия с внешней средой имеем уравнение
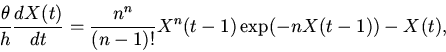\begin{displaymath} \frac{\theta}{h}\frac{dX(t)}{dt}= \frac{n^{n}}{(n-1)!}X^{n}(t-1)\exp(-nX(t-1))-X(t), \end{displaymath} (7)

которое при достаточно больших сопряженностях, на основе формулы Стирлинга  [19], может быть написано в виде
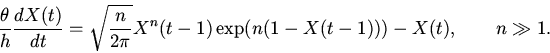\begin{displaymath} \frac{\theta}{h}\frac{dX(t)}{dt}= \sqrt{\frac{n}{2\pi}}X^{n}(t-1)\exp(n(1-X(t-1)))-X(t), \qquad n \gg 1. \end{displaymath} (8)

Здесь $X(t)$ - величина, характеризующая количество сигнала $or$; $\theta$ - постоянная, характеризующая среднее время существования сигналов; $h$ - среднее время обратной связи; $n$ - степень самосопряжения  [18,19].

Качественное исследование

Обычно математические модели включают количественное описание функционирования моделируемого объекта или явления на основе математических уравнений. Однако, только составление уравнений и сами уравнения не являются еще математической моделью. Необходимым звеном математического моделирования регуляторных систем является определение наиболее общих свойств поведения решений рассматриваемых уравнений - качественное исследование соответствующих уравнений  [19].

Анализ характера решений уравнений (8), на основе методов качественного исследования функционально-дифференциальных уравнений  [16,18,19], показывает нахождение их решений в первом квадранте фазового пространства при неотрицательности значений параметров и начальных условий; неустойчивость бесконечно удаленных точек; возможность существования тривиального и нетривиальных положений равновесия. Поведение решений в области нетривиального положения равновесия, являющегося функционально активным состоянием регуляторной системы, может носить характер устойчивых стационарных режимов, предельных циклов типа Пуанкаре и сложных колебаний  [14].

Рассмотрим некоторые основные закономерности функционирования регуляторных механизмов (регуляторики) самосопряженных систем на основе качественного анализа уравнений (8).

Если примем, что, в случае нормальной регуляторики, сигналы, вырабатываемые $or$ и в среднем существующие $\theta$ единиц времени, должны "дожить'' до осуществления петли обратной связи (т.е. $\theta=h$), то для них (8) примет вид

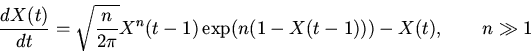\begin{displaymath} \frac{dX(t)}{dt}= \sqrt{\frac{n}{2\pi}}X^{n}(t-1)\exp(n(1-X(t-1)))-X(t), \qquad n \gg 1 \end{displaymath} (9)

которое не содержит постоянных, кроме величины самосопряжения.

Случай $\theta > h$, когда сигнал (продукт активности $or$) может участвовать в регуляции $orasta$ более чем один раз (т.к. сигнал живет дольше по сравнению со временем, необходимым для осуществления петли обратной связи), мы можем назвать сильной регуляторикой. Тогда естественно назвать слабой регуляторикой случай $\theta < h$. При очень слабой регуляторике ($\theta \ll h$) для предварительного качественного анализа рассматриваемых регуляторных систем может быть полезно следующее функциональное уравнение регуляторики самосопряженных систем  [18,19]

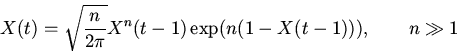\begin{displaymath} X(t)= \sqrt{\frac{n}{2\pi}}X^{n}(t-1)\exp(n(1-X(t-1))), \qquad n \gg 1 \end{displaymath} (10)

и его дискретный аналог
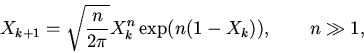\begin{displaymath} X_{k+1}= \sqrt{\frac{n}{2\pi}}X^{n}_{k}\exp(n(1-X_{k})), \qquad n \gg 1, \end{displaymath} (11)

где $X_{k}$ - величина, выражающая число сигналов, вырабатываемых $or$ на $k$-ом шаге жизнедеятельности $orasta$. Величина шага в данном случае соответствует времени, необходимого для осуществления петли обратной связи в рассматриваемой $orasta$ (единице времени $orasta$).

Условие существования стационарных режимов функционирования нетривиальных (положений равновесия в первом квадранте фазового пространства) для рассматриваемых систем выражается в виде

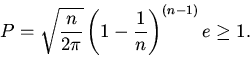\begin{displaymath} P=\sqrt{\frac{n}{2\pi}}\left(1-\frac{1}{n}\right)^{(n-1)}e\geq 1. \end{displaymath} (12)

При $Р<1$ имеется только тривиальное положение равновесия. Нетривиальное положение равновесия возникает, путем жесткого возбуждения, при $P=1$ в точке $C = (n-1)/n$. Рост значения $P$ приводит к бифуркации положения равновесия $C$ на два нетривиальных положений равновесия $(A,B)$, постепенно удаляющихся от точки $C$ на две стороны. Расчеты на ЭВМ показывают (с учетом принятого приближения, на основе формулы Стирлинга для больших $n$  [19]), что нетривиальные положения равновесия самосопряженных регуляториных систем возникают при $n \geq 6$ и, по мере роста $n$, вначале удаляются от точки $C$, затем сближаются друг с другом, оставаясь в разных сторонах от $С$.

Рассмотрим устойчивость положений равновесия при $n \geq 6$. Очевидна устойчивость тривиального положения равновесия. Использование метода Ляпунова, путем линеаризации (8) около нетривиального положения равновесия $\xi$, приводит к характеристическому уравнению

\begin{displaymath} (\theta \lambda + h) e^{\lambda}+hn(1-\xi)=0. \end{displaymath}

Отрицательность вещественной части корней данного трансцендентного уравнения могут быть исследованы на основе критерия Хейса  [5,19]

\begin{displaymath} h+\theta >0; \end{displaymath}


\begin{displaymath} 1+n(\xi-1)>0; \end{displaymath} (13)


\begin{displaymath} hn(\xi-1)<\theta\mu\sin(\mu)-h\cos(\mu), \end{displaymath}

где $\mu$ - корень уравнения

\begin{displaymath} \theta \mu=-htg \mu, \qquad 0<h< \theta \pi. \end{displaymath}

Первое условие (13) для рассматриваемых уравнений всегда выполняется, а второе сводится к $\xi > (n-1)/n$ и выполняется только для $B$, которое является аттрактором в $(A,\infty)$. Следовательно, положение равновесия $А$ является неустойчивым и функционально активной областью рассматриваемой регуляторной системы является сфера действия аттрактора $В$. Для $B$ третье условие (13), в случае нормальной регуляторики, сводится к $\xi < 2.24/n+1$, которое выполняется не всегда. Как показывают конкретные расчеты, для $6 \leq n \leq 8$ имеем устойчивость $B$, а для $n>8$ - неустойчивость. Потеря устойчивости сопровождается появлением колебаний вокруг $В$.

Для случая систем с очень слабой регуляторикой получаем условие устойчивости $B$ в виде неравенства $\xi <1+1/n$. Как показывают расчеты, уже для $n = 9$ оно не выполняется, т.е. при $n \geq 9$ устойчивость положения равновесия в точке $B$ нарушается. Результаты качественного исследования решений (11) в области неустойчивости показывают существование довольно сложного диапазона поведения рассматриваемой модели самосопряженных регуляторных систем. Помимо периодических режимов функционирования, возможны нерегулярные колебания и эффект "черная дыра''  [19]. Последний заключается в возникновении деструктивных изменений в моделируемой системе и выражается срывом колебаний - стремлением решений к тривиальному положению равновесия. Расчеты, проведенные на ПЭВМ с помощью вычисления Ляпуновской величины, информационоой и высших размерностей решений, построения диаграмм Кенингса-Ламерея (11), показывают существование нерегулярных колебаний при $n \geq 9$ и наступление эффекта "черная дыра'' при $n>12$. Следовательно, стабильные самосопряженные регуляторные системы с очень слабой регуляторикой, находящиеся в равновесии с внешней средой, могут существовать только при $6 \leq n \leq 12$  [18,19].

Применение результатов

Данный метод количественного исследования регуляторных механизмов живых систем был применен для решения некоторых медико-биологических задач совместно с соответствующими специалистами  [1,14,15,17,20]. Приведем результаты модельного исследования механизмов роста микроорганизмов  [14] и возникновения злокачественных новообразований  [20].

В первом случае рассматривались закономерности роста клеток хлореллы в связи с задачей оптимизации их выращивания  [14]. Применение рассматриваемого подхода показало, что онтогенез хлореллы (рост молодой клетки (до материнской) $\Rightarrow$ деление-дробление $\Rightarrow$ выход молодых клеток хлореллы во внешнюю среду) сопровождается увеличением самосопряженности популяции клеток при размножении. Достижение самосопряженности (количества клеток) порогового значения (12) приводит к эффекту "черная дыра'', т.е. к распаду системы, что и наблюдается при экспериментах после 4- 5-ти кратного деления  [14].

Во втором случае был проведен анализ механизмов возникновения злокачественного новообразования. Была рассмотрена гипотеза об управлени ранним эмбриональным развитием посредством продуктов (и-РНК) генетической Системы Автономного Развития (САР). САР функционирует на этапе "ламповых щеток'' оогенеза для образования необходимого количества соответствующих и-РНК (и хранящихся в виде информасом). Они используются, после оплодотворения, для обеспечения развития зародыша автономно от материнского организма до включения собственного генома (обычно до гаструлы  [17]). Как показали результаты модельных исследований на основе рассматриваемых уравнений регуляторики живых систем  [20], САР может состоять из нескольких блоков (инициации, образования и-РНК и репрессии) и жестко блокируется после оогенеза. Деблокировка САР, на основе внутренних и внешних причин, приводит к появлению последовательных залпов генетической информации САР и развитию автономных клеток, которые могут дать начало злокачественному росту  [17,20]. Продукты блока инициации, возникающие до автономного развития, могут быть использованы для раннего обнаружения активации САР, а продукты блока репрессии - для подавления функциональной САР  [17,20].

Резюме

Моделирование регуляторики живых систем с учетом кооперативности процессов, наличия временных взаимоотношений и комбинированной обратной связи приводит к системе дифференциально-разностных уравнений. Результаты качественного анализа показывают наличие режимов покоя и функционально активного состояния, неустойчивости бесконечно удаленных точек и нахождение решений в первом квадранте фазового пространства при положительных значениях начальных условий и параметров. Исследование поведения самосопряженных регуляторных систем на основе их дискретных уравнений (11) показывает возможность существования нерегулярных колебаний и деструктивных изменений в регуляторных системах - эффекта "черная дыра''. "Черная дыра'' ограничивает число возможных вариантов стабильных самосопряженных регуляторных систем.

В условиях равновесия с внешней средой самосопряженная регуляторная система, с очень слабой регуляторикой, обладает семью вариантами стабильного существования, когда степень самосопряжения принимает значения от шести до двенадцати. Более высокие сопряженности могут существовать при организации иерархических регуляторных систем (что и наблюдается в реальных условиях). Использование данного подхода модельного исследования регуляторных систем для анализа механизмов развития микроорганизмов  [14,15] и ракового новообразования  [1,20] показало его приемлемость при количественном исследовании механизмов регуляции биосистем.

Литература

1
Hidirov B.N., Saidalieva M. Modeling of genetic mechanism of cancer //Proceedings of the Ninth World Congress on Medical Informatics. Korea, Seoul, 1998, 397.

2
Tsanev R., Sendov Bl. A model of the regular mechanism of cellular miltiplication //J. Theor. Biol., 12, 1966, 327.

3
Берг Р.С., Тимофеев-Ресовский Н.В. О путях эволюции генотипа //Проблемы кибернетики. М., 5, 1961, 183-197.

4
Винер Н. Кибернетика или управление и связь в животном и машине. М. Советское радио, 1958.

5
Гласс Л., Мэки М. От часов к хаосу. Ритмы жизни. . М.: Мир, 1991, 107.

6
Гудвин Б. Временная организация клетки. М.: Мир, 1966, 59-70.

7
Ляпунов А.А. О некоторых общих вопросах кибер- нетики //Проблемы кибернетики, 1, 1958, 5-22.

8
Полетаев И.А. Сигнал. : Советское радио, 1958.

9
Ратнер В.А. Генетические управляющие системы. Новосибирск "Наука'', 1966.

10
Ратнер В.А. Молекулярно-генетические системы управления Новосибирск "Наука'', 1975.

11
Ратнер В.А., Шамин В.В. Сайзеры: моделирование фундаментальных особенностей молекулярно-биологической организации. I. Сайзера с несцепленными матрицами //Математические модели эволюционной генетики, Новосибирск, Изд-во ИЦ и ГСО АН СССР, 1980, 60-82.

12
Сайдалиева М. Моделирование клеточных сообществ //Вопросы кибернетики, 103, Ташкент, 1978, 89-103.

13
Сендов Б., Цанев Р. и Матеева В. Исследоване на един математически модел на регуляцията на клетъчного размножение в епидермиса //Известия на математическия институт "Болгарска Академия на науките'', XXI, 1966, 221.

14
Халмурадов А.Г., Хидиров Б.Н., Расулов А.С., Сайдалиева М. Модельные исследования механизмов регуляции глутаминсинтетазной активности одноклеточных зеленых водорослей //ДАН РУз, 8-9, Ташкент, 1991, 85-87.

15
Халмурадов А.Г. Хидиров Б.Н., Сайдалиева М., Буриев С.Б., Ахунов А.А. Исследование регуляторных механизмов жизнедеятельности микроорганизмов количественными методами //Узбекский биологический журнал, 1, Ташкент, 1993, 22-25.

16
Хидиров Б.Н. Об одной биологической краевой задаче дифференциально-разностных уравнений //Вопросы кибернетики. РИСО АН УзССР, 76, Ташкент, 1975. 132-137.

17
Хидиров Б.Н. Возможная модель возникновения злокачественных новообразований //Вопросы кибернетики. РИСО АН УзССР, 88, Ташкент, 1976, 85-89.

18
Хидиров Б.Н. Об одном методе исследования регуляторики живых систем //Вопросы кибернетики. РИСО АН РУз, 128, Ташкент, 1984, 41- 46.

19
Хидиров Б.Н. Исследование регуляторики живых систем //Вопросы кибернетики. РИСО АН РУз, 132, Ташкент, 1986, 57-60.

20
Хидиров Б.Н., Сайдалиева М. Моделирование генетических механизмов рака //ДАН РУз , 9, Ташкент, 1997, 35-38.

21
Эйген М., Шустер П. Гиперцикл. Принципы самоорганизации макромолекул. М.: Мир. 1982, 34.

Примечание

... систем 1
Работа частично поддержана грантами 40-96 и 61-00 Фонда фундаментальных исследований АН РУз.
Ваши комментарии
[SBRAS]
[Головная страница]
[Конференции]
[СО РАН]

© 2001, Сибирское отделение Российской академии наук, Новосибирск
© 2001, Объединенный институт информатики СО РАН, Новосибирск
© 2001, Институт вычислительных технологий СО РАН, Новосибирск
© 2001, Институт систем информатики СО РАН, Новосибирск
© 2001, Институт математики СО РАН, Новосибирск
© 2001, Институт цитологии и генетики СО РАН, Новосибирск
© 2001, Институт вычислительной математики и математической геофизики СО РАН, Новосибирск
© 2001, Новосибирский государственный университет
Дата последней модификации Tuesday, 11-Sep-2001 19:18:44 NOVST