Клеточно-нейронный автомат - дискретная модель динамики активных сред 1

Бандман О.Л.
Институт вычислительной математики и математической геофизики СО РАН, Новосибирск

Аннотация:

Предлагается параллельный алгоритм мелкозернистого типа для моделирования процессов пространственной динамики в активных средах. Алгоритм объединяет в единую итерационную процедуру клеточно-автоматный метод моделирования диффузионной части процесса и клеточно-нейронный метод - для моделирования влияния активной среды. Последний основан на новой модели "вероятностного нейрона''. Предложены способы преобразования непрерывной пространственной функции в ее дискретный эквивалент в виде булева массива (булева дискретизация) и обратного преобразования булева пространства в вещественную функцию (осреднение). Такой "гибридный'' (дискретный + непрерывный) алгоритм абсолютно устойчив к ошибкам округления и допускает естественное распараллеливание. Приведены примеры моделирования распространения нелинейных волн в экологических системах.


A fine-grained parallel algorithm is proposed, which is intended for simulation spatial dynamics in active media. The algorithm combines into a single iterative procedure Boolean operations of Cellular Automaton Diffusion with Cellular-Neural simulation of nonlinear reaction of active medium. Methods for transforming a continuous spatial function into its boolean equivalent (Boolean discretization), and the inverse methods to transform a Boolean space into a function in real numbers (averaging) are elaborated to be used on each iteration. Such a "hybrid'' (discrete + continuous) algorithm is absolutely stable relative to round off errors and allows natural parallelization. Examples are given to show simulation of nonlinear waves in ecological system.

1. Введение

В связи с появлением многопроцессорных вычислительных систем и суперкомпьютеров активизируется поиск таких математических моделей пространственной динамики, которые легко распараллеливаются. В частности, большой интерес проявляется к дискретным моделям, обладающим свойствами мелкозернистого параллелизма. Интенсивно изучаются клеточные автоматы моделирующие диффузию [8,2] и газовую динамику [4]. Имеется также ряд попыток построить клеточно-автоматные модели кинетики и химических процессов [5]. Такие модели рассматриваются как "альтернатива (а не аппроксимация) дифференциальных уравнений в частных производных'' [3], поскольку имеют по сравнению с ними ряд преимуществ: отсутствие ошибок округления и абсолютную вычислительную устойчивость. Клеточный автомат (КА), моделирующий физическое явление, отражает его свойства на микроскопическом уровне взаимодействия частиц. Булевы состояния клеток КА соответствуют существованию или отсутствию абстрактной частицы (молекулы, компоненты скорости, единицы плотности, концентрации популяции и т.д.) в определенной точке и в определенный момент. Функции, выполняемые клетками (правила переходов элементарных автоматов), строятся а основе анализа моделируемого явления. Переход от булевых к физическим величинам производится с помощью процедуры осреднения по некоторой окрестности каждой клетки. Клеточно-автоматные модели природных явлений еще недостаточно изучены. Существует масса проблем, которые нужно решить, прежде чем они войдут в практику. В частности, для каждой модели необходимо доказать (или показать), что эволюция клеточного автомата соответствует динамике моделируемого процесса, и найти способ учета физических параметров (плотности, вязкости, теплопроводности среды, химической активности и др.). Эти проблемы были решены теоретически только для двух моделей: для КА-диффузии [8] и для КА газовой динамики [4] (Gas-Lattice model). Для процессов в активных средах КА-модели находятся в стадии изучения и экспериментирования.

Процессы динамики в активных средах (реакционно-диффузионные процессы в физике, химии, биологии, экологии [6,7]) традиционно представляются дифференциальными уравнениями (или системами уравнений) с частными производными. Правая часть этих уравнений состоит из двух частей: диффузионной, представленной лапласианом, и реакционной, представленной нелинейной функцией, отображающей активную составляющую. Уравнения этого типа изучаются "поштучно'' и с большим трудом, так как аналитические решения получить невозможно из-за нелинейного члена, а численные методы либо плохо распараллеливаются (неявные схемы решений), либо ограничены условиями устойчивости и точности (явные схемы). А между тем алгоритмы КА-диффузии таких ограничений не имеют. Они достаточно хорошо разработаны и теоретически обоснованы [8,2]. Отсюда вытекает стремление использовать дискретные КА- алгоритмы для моделирования диффузионной составляющей и клеточно-нейронную (КН) модель [5] - для нелинейной реакции. В статье предлагается такая "гибридная'' модель и делается попытка ее обосновать теоретически и подтвердить экспериментально.

Кроме введения, статья содержит 4 раздела и заключение. Во втором разделе дана формальная постановка задачи и общая схема предлагаемого алгоритма. В третьем разделе представлены методы КА-диффузии и КН-реакции. В четвертом - приведены результаты экспериментов. В заключении намечены проблемы для дальнейших исследований.

2. Постановка задачи и схема ее решения

2.1. Непрерывное и дискретное представления реакционно-диффузионных процессов

Традиционно процессы типа "реакция-диффузия'' задаются системами дифференциальных уравнений с частными производными вида
\begin{displaymath} \frac{du}{dt} = d(\frac{\partial^2 u}{\partial x^2}) + F(u) \end{displaymath} (1)

где $u$ переменная величина, условно называемая концентрацией с областью значений в интервале (0,1), $t,x$ - временная и пространственная переменные, $d$ - коэффициент диффузии, $F(u)$ дифференцируемая нелинейная функция, обычно задаваемая полиномами, и за пределами интервала $(0,1)$ равная $0$. В классической работе [7] использована функция вида (рис.1a)
\begin{displaymath} F(u)=\alpha u(1-u); \end{displaymath} (2)

При начальных условиях вида
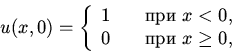\begin{displaymath} u(x,0) = \left\{\begin{array}{ll} 1 &\quad \mbox{при} \ x<0, \\ 0 & \quad \mbox{при} \ x\geq 0, \end{array} \right . \end{displaymath} (3)

уравнение (1) описывает автоволновой процесс типа бегущий фронт, который моделирует автокаталитические процессы, распространение огня, эпидемий, сорняков и т.д. В [10] приведены аналитически определенные скорость распространения фронта и форма волны. При $t\rightarrow \infty$ они равны
\begin{displaymath} v^0 =2 \sqrt{d \alpha}, \quad u(x) =\frac{1}{1-e^{-Cx}}, \quad \mbox{где} \ \ C=\sqrt{2 \alpha}. \end{displaymath} (4)

В исследованиях по экологии функции, удовлетворяющие условиям (2), называются логистическими и считаются базовыми, хотя применяются также полиномы третьей степени (рис.1b)

\begin{displaymath} F(u)=\alpha u(1-u)(u-u_1), \ \ 0<u_1<1, \end{displaymath} (5)

Рис. 1: Нелинейные функции в диффепенциальных уравнениях экологических систем
\begin{figure} \begin{center} \epsfxsize=12cm\ %%\epsfysize=12cm \epsfbox{fif1.eps} \epsfbox{fif2.eps} \end{center} \end{figure}

При начальных условиях (3) и $F(u)$ вида (5) скорость бегущего фронта

\begin{displaymath} v=\sqrt{\alpha/2}(1-2u_1) \end{displaymath} (6)

Кроме того, при начальных условиях, называемых ''вспышкой'', т.е.
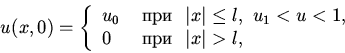\begin{displaymath} u(x,0) = \left \{\begin{array}{ll} u_0 \ & \mbox{при} \ \... ... 0 \ & \mbox{при} \ \ \vert x\vert> l, \end{array} \right. \end{displaymath} (7)

если $l$ и $u_{max}$ недостаточно велики, то бегущего фронта не образуется и вспышка затухает.

Уравнения второго порядка моделируют более сложные явления (химические реакции, распространение волн, эпидемий, образование вихрей и др.) Например, модель Тайсона-Файфа реакции Белоусова--Жаботинского [6], порождающей концентрические расходящиеся волны.

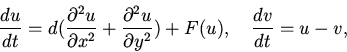\begin{displaymath} \frac{du}{dt}= d(\frac{\partial^2 u}{\partial x^2}+ \frac{... ...tial^2 u}{\partial y^2}) + F(u), \quad \frac{dv}{dt} = u-v, \end{displaymath} (8)

где

\begin{displaymath} F(u)=\frac{1}{d}(u(1-u)-fv(u-q)/(u+q)), \end{displaymath}

$q$ - исходная концентрации плотности веществ в среде $(u(0)=q, v(0)=q)$, $f(x,y)$ - пространственная функция изменения исходной концентрации, вызывающая возникновение волн, $(1/2u<f(0)<(1-q)<f(\infty))$, $d$ - коэффициент диффузии.

Представленные выше примеры реакционно-диффузионных уравнений и их известных свойств затем будут использованы для сравнения с аналогичными свойствами, полученными с помощью модели клеточно-нейронного автомата.

Как и для конечно-разностных методов решения дифференциальных уравнений с частными производными, КН-модель содержит процедуры дискретизации пространственных координат и времени, так что $x=hi, y=hj, t=n\tau, i,j,h=\{0,1,\ldots,\}$. При $h=1, n=1$ уравнение (1) приобретает вид

\begin{displaymath} u_{ij}(n+1) = u_{ij}(t)+dL(u_{ij}) + F(u_{ij}), \end{displaymath} (9)

где
\begin{displaymath} L(u_{ij}=u_{i-1,j}+u_{i+1,j}+u_{j-1,i}+u_{j=1,i}-4u_{ij} \end{displaymath} (10)

дискретное представление оператора Лапласа над $u_{ij}$.

Клеточно-нейронная модель (также как и автоматная) имеют дело с дискретными величинами основной переменной, которые являются "предельно дискретными'', т.е. булевыми. Поскольку КН-автомат использует и дискретные и непрерывные переменные, то для описания его работы далее применяются Формализмы универсальной модели клеточных Вычислений - алгоритма параллельных подстановок (АПП) [1]. В этой модели функция $u(i,j)$ представляется в виде клеточного множества $U=\{(a,m)\}$, элементами которого служат пары вида $(a,m)$, называемые клетками. В них $a\in$ A - символ алфавита A, обозначающий состояние клетки, а $m \in$ M - имя клетки из множества имен M. Множество имен (в общем случае, счетное), обычно, состоит из номеров клеток или наборов пространственных координат. Например, если функция $u(i,j)$ определена в двумерном декартовом пространстве $(0<i<p, \ 0<j<q)$, то множество имен M $=\{[ i,j]: i=0,\ldots,p-1; j=0,\ldots,q-1\}$. В каждой точке с именем $[ i,j]$ значение функции $u_{ij}$ является состоянием клетки $[ i,j]$.

Операции над клеточными множествами задаются системами параллельных подстановок вида

\begin{displaymath} \Theta: C(m)*S(m) \rightarrow S^\prime(m), \quad \mbox{для всех} \ \ m\in M, \end{displaymath} (11)

где
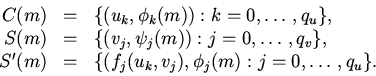\begin{displaymath} \begin{array}{rll} C(m)& =& \{(u_{k},\phi_{k}(m)): k=0, \l... ...(f_{j}(u_k,v_j),\phi_{j}(m): j=0, \ldots, q_u\}, \end{array} \end{displaymath} (12)

В (11) и (12) $C(m), S(m)$ и $S^\prime(m)$ - локальные конфигурации с центром в клетке с именем $m \in M$, а знак "$\ast$ " означает объединение конфигураций. $u_{k}, v_{j}$ - переменные состояний или константы, а $f_{j}(u_k,v_j)$ - функции клеток с областью определения в A. Функции $\phi_{k}(m))$ и $\psi_{j}(m)$ называются именующими, они определяют имена клеток-соседей для центральной клетки $m$.

Параллельные подстановки применяются все одновременно и параллельно ко всем тем клеткам клеточного множества, для которых локальная конфигурация совпадает с левой частью подстановки. В результате их применения состояния клеток базовой части $S(m)$ заменяются на результат вычисления функций $f(u,v)$. Клетки локальной конфигурации $C(m)$, называемой контекстом не меняют состояний. Такое итерационное применение подстановок моделирует эволюцию клеточного множества и продолжается до тех пор, пока система не придет в устойчивое состояние.

2.2. Общая схема алгоритм работы клеточно-нейронного автомата

КН-автомат - это автомномная система локально связанных клеток. Алгоритм его работы итерационный: на каждой итерация все клетки выполняют определенную процедуру над состояниями некоторого множества связанных с ней соседей и, в зависимости от результата, меняют или не меняют свое состояние.

Исходное состояние может быть задано клеточным множеством $U_0=\{(u_m,m)\}$, где $u_m \in$A - булевы константы. или вещественной функцией $w(m)$ в дискретизированном пространстве. В первом случае чтобы получить вещественные значения необходимо выполнить над $U_0$ подстановку $U_0^\prime=\{(u_m^\prime,m)\}$, где $u_m^\prime \in$R, в котором значения $u_m^\prime$ получены путем применения процедуры осреднения, $\Theta_{av}(U_0)=u_0^\prime$

\begin{displaymath} \Theta_{av}: \{(u_k,\phi_k(m)): k=1,\ldots,\vert Q\vert\} \ast \{(u_m,m)\}\rightarrow \{(u^\prime_m,m)\}, \end{displaymath}

где
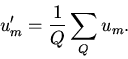\begin{displaymath} u^\prime_m = \frac{1}{Q}\sum_{Q}{u_m}. \end{displaymath} (13)

Здесь $\vert Q\vert$ - мощность окрестности осреднения $Q=\{ \phi_k(m)\}$. Во втором случае следует выполнить булеву дискретизацию - вещественной пространственной функции булевым клеточным множеством (разделе 3.3).

Функционирование КН-автомата моделирует итерационнный алгоритм конечно-разностного уравнения (10), на каждом шаге вычисляя первые два члена правой части как КА-диффузию, и третий член как ''клеточно-нейронную реакцию''. Формально работа КН-автомата описывается следующим образом. Пусть результат $t$-го шага в булевом представлении равен клеточному множеству $U(t)=\{(u_m,m): u_m \in \{0,1\}, m\in M$. Один итерационный шаг КН-автомата состоит из следующих двух операций.

1. Выполнение одного шага КА-диффузии (раздел 3.1).

\begin{displaymath} U_D(t+1) = \Phi(U(t)), \end{displaymath}

2. Выполнение одного шага клеточно-нейронной реакции. При этом клетка выполняет функцию вероятностного нейрона (раздел 3.2), которая состоит в том, чтобы изменить булево состояние клетки в зависимости от значения $F(u_m^\prime(t))$.

3. Функциональное описание КН-автомата

3.1. Клеточно-автоматная диффузия

Существует несколько хорошо разработанных методов КА-диффузии [2]. Наиболее изученным и теоретически обоснованным является метод, названный в [2] методом поворота блоков (ПБ-диффузия), а в [8] - КА с окрестностью Марголуса. Далее приводится двумерный случай, который естественным образом может быть редуцирован к одномерному или трехмерному. Метод состоит в следующем.

Исходным является клеточное множество $U=\{(u_{ij},[i,j]): [i,j]\in M, u_{ij} \in \{0,1\} \}$, которое может быть получено путем применения процедуры булевой дискретизации к заданной пространственной функции распределения концентрации. Строится два разбиения множества имен M{[i,j]}на блоки, размером 2х2: четное разбиение, в котором диагональные клетки блоков имеют четную сумму координат ($i+j=2k$), и нечетное, в котором диагональные клетки блоков имеют нечетную сумму координат ($i+j=2k+1$). Каждая итерация алгоритма разделена на два шага. На четных шагах клеточно-автоматное правило перехода применяется к четным блокам, на нечетных - то же самое правило применяется к нечетным. Правило состоит в следующем. На каждом четном (нечетном) шаге все четные (нечетные) блоки поворачиваются на $\pi/2$ по часовой или против часовой стрелки с равной вероятностью. В терминах АПП это выражается формально в виде системы из двух подстановок $\Phi=\{\Theta_1,\Theta_2\}$, где

\begin{displaymath} \left \{ \begin{array}{lll} \Theta_1:& \{(rand(1)<p,[i,j]... ...), (u_3,[i+1,j+1]), (u_0,[i+1,j]), \\ \end{array} \right. \end{displaymath} (14)

Здесь $rand(1)$ - случайное число в интервале (0,1), $[i,j]^\prime$ - имя контекстной клетки, $p$ - вероятность. При $p=1/2$ коэффициент диффузии равен $d=3/2$ [8]. Изменением значений вероятности и шагов дискретизации можно получить другое значение $d$.

Одномерный ПБ-метод отличается от двумерного тем, что блоки в нем состоят из пар клеток, причем четные (нечетные) блоки имеют четное (нечетное) имя левой клетки. На четных (нечетных) шагах клетки четных (нечетных) блоков обмениваются состояниями.

3.2. Клеточно-нейронная реакция

При выполнении функции КН-реакции клетки работают как вероятностные нейроны. Понятие вероятностного нейрона является новым. Его отличие от общеизвестного "искусственного нейрона'' [9] состоит в том, что нелинейная функция от суммы взвешенных входов выполняется с некоторой вероятностью, а веса связей равны $1$. В клеточно-нейронном автомате вероятностный нейрон выполняет следующую параллельную подстановку.
\begin{displaymath} \Theta_3: \{(u_k, \phi_k(m)):k=1,\ldots,\vert Q\vert\}\ast \{(u_m,m)\} \rightarrow \{(u_m(t+1),u_m),m)\} \end{displaymath} (15)

где $u_k$ - состояниe $k$-го элемента окрестности осреднения $Q$, а
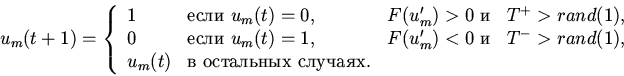\begin{displaymath} u_m(t+1)= \left\{ \begin{array}{llll} 1 & \mbox{если}\ u... ... u_m(t) & \mbox{в остальных случаях}. && \end{array} \right. \end{displaymath} (16)

В (17) $T^+$ и $ T^-$ - вероятности того, что клетка должна изменить состояние $u_m=0$ на $u_m=1$ и $u_m=1$ на $u_m=0$, соответственно.
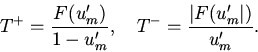\begin{displaymath} T^+ = \frac{F(u_m^\prime)}{1-u_m^\prime},\quad T^- = \frac{\vert F(u_m^\prime\vert)}{u_m^\prime}. \end{displaymath} (17)

Поскольку нелинейный (реакционный) член во многих экологических задачах имеет вид полинома, в котором имеется сомножитель вида $(1-u_m^\prime)$, равный вероятности того, что $u_m^\prime=0$, то функции $T^+$ и $ T^-$ упрощаются. Например, если $F(u)$ имеет вид (3), то $T^+=\alpha u_m^\prime$.

3.3. Булева дискретизация вещественной функции

Очевидно, что вероятностный нейрон не дает точного значения реакционной составляющей, а аппроксимирует ее, одновременно выполняя булеву дискретизацию. Задача булевой дискретизации состоит в том, чтобы по вещественной функции $w(m)$, определенной в дискретном пространстве, построить клеточное множество $U=\{(u_m,m)\}$ с булевым алфавитом B=$\{0,1\}$ такое, чтобы для каждой клетки осредненное значение $u_m\prime$, вычисленное по (13), как можно меньше отличалось бы от $w(m)$, т.е.
\begin{displaymath} w(m) - u_m\prime < \epsilon, \end{displaymath} (18)

где $\epsilon \ll Q$ - погрешность булевой дискретизации. Далее предполагается, что никаких других погрешностей (погрешность округления, погрешность пространственной дискретизации) не существует. Такое предположение оправдано целью анализа влияния погрешности предлагаемого метода.

Точного решения поставленная задача не имеет. Приближенно она решается следующим образом. Состояние каждой клетки определяется из условия: вероятность того, что оно равно 1 равна $w(m)$

\begin{displaymath} p_{(u_m=1)}=w(m). \end{displaymath} (19)

При этом математическое ожидание того, что осредненное состояние $u_m\prime=w_m,$ будет равно осредненной сумме вероятностей, т.е.
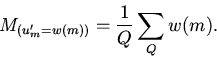\begin{displaymath} M_{(u_m^\prime=w(m))}=\frac{1}{Q}\sum_Q{w(m)}. \end{displaymath} (20)

Предположим, что функция в области соседства клетки постоянна, т.е. $w(m)=c$. Тогда, согласно (20) и (21) $M_{(u_m^\prime=w(m)}=u_m^\prime$. Следовательно, в этом вырожденном случае ошибка булевой дискретизации $e(m)=0$. Пусть среднее отклонение состояний клеток в окрестности осреднения

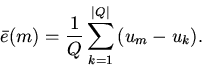\begin{displaymath} \bar{e}(m)=\frac{1}{Q}\sum_{k=1}^{\vert Q\vert}{(u_{m}-u_k)}. \end{displaymath} (21)

Тогда матeматическое ожидание того, что $u_m\prime=w(m)$
\begin{displaymath} M_{{u_m\prime=w(m)}} = u_m\prime+\bar{e}(m), \end{displaymath} (22)

т.е. $\bar{e}(m)$ равно ошибке булевой дискретизации в точке $m$.

Из (22) можно сделать заключение, что если функция имеет постоянную пространственную производную в окрестности осреднения точки $m$ (функция $w(m)$ линейна), то $\bar{e}(m)=0$, так как положительные и отрицательные отклонения компенсируют друг друга. По той же причине $\bar{e}(m)=0$ для функций вида $w(m)=am^3+с$, ($a,c$ - произвольные константы) и всех остальных парабол нечетной степени.

Точность булевой дискретизации зависит от выбора двух параметров:

1) размеров пространственного шага (будем считать что он одинаков по всем координатным направлениям и равен $h$),

2) мощности окрестности осреднения $\vert Q\vert$, которая в случае 1D равна $2r$, а в случае 2D равеа $4r^2$ ($r$-радиус осреднения).

Эти параметры должны быть выбраны так, чтобы, с одной стороны, минимизировать "автоматный шум'', и, с другой стороны, чтобы была минимальной ошибка осреднения. Эти два требования противоречивы, первое требует большой окрестности, второе - маленькой.

Требование малого автоматного шума может быть выражено следующим образом:

\begin{displaymath} \alpha/Q < \epsilon, \quad k=1,2,...,\vert Q\vert. \end{displaymath} (23)

Это означает, что наличие $\alpha$ неправильных булевых значений в окрестности не должны привести к превышению заданного порога неточности. При обычных требованиях можно принять $\alpha=1$.

Требование малой ошибки осреднения формулируется исходя из того, что на каждом пространственном шаге отклонение от от средней ошибки равно

\begin{displaymath}e_m(h)=h(\frac{dw}{dx}(i)-\frac{dw}{dx}(i+h))/2=h (\Delta w^\prime)/2\end{displaymath}

т.е. пропорционально разности производных. При этом в окрестности клетки с именем $m=x/h$ погрешность не превысит
\begin{displaymath} e(Q_m)\leq (\Delta w^\prime)_{max} hr/2, \end{displaymath} (24)

где $(\Delta w^\prime)_{max}$ - наибольшая в пределах окрестности разность значений пространственной производной. Отсюда
\begin{displaymath} (\Delta w^\prime_{max}) hr/2 < \epsilon \end{displaymath} (25)

Комбинируя (23) и (25), получим условие, обеспечивающее точность аппроксимации в виде следующих соотношения:
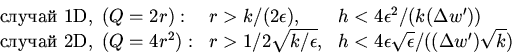\begin{displaymath} \begin{array}{lll} \mbox{случай 1D}, \ (Q=2r):& r>k/(2\eps... ...lon\sqrt{\epsilon}/((\Delta w^\prime) \sqrt{k})\\ \end{array} \end{displaymath} (26)

4. Результаты моделирования

Одномерный бегущий фронт

Моделировался процесс распространения концентрации, описанный типовым уравнением (1), c реакционной составляющей вида (2) при $d=0,75 $, $\alpha =0,5 $ и начальными условиями типа "вспышки''. Размеры клеточного множества 32х256 клеток. Распространение фронта происходит вдоль оси $j$, $-128<j<128$. В каждом подмножестве клеток с $i=const, i=0,\ldots,31$, (строке клеточной структуры) выполняется алгоритм одномерной КА-диффузии. Осреднение (вычисление $u_m^\prime$) по окрестности $Q=\{[0,j-10],\ldots, [15,j+10]\}$. Функции КН-реакции вычисляется по алгоритму вероятностного нейрона (16) с вероятностями $T^+=\alpha u_m^\prime$. По расстояниями между фронтами при разных $t$ определялась скорость распространения, которая постепенно увеличивалась с увеличением времени, начиная с $v=2,6$ при $t=20$ и кончая $v=1,4$ при $t=80$, (рис.2.a) (для сравнения по формуле (4) $v(t=\infty)=1,2)$. Форма фронта совпадает с расчитанной по (4) с точностью до $3\%$. То же уравнение c теми же начальными условиями и параметрами моделирования, но с $F(u)$ вида (5) дали затухающую вспышку (рис.2b).

Рис. 2: Распространение бегущего фронта. а) Осредненные кривые $u^\prime(j)$, b) затухающая вспышка
\begin{figure} \begin{center} \epsfxsize=12cm\ %%\epsfysize=12cm \epsfbox{liap0.eps} \end{center} \end{figure}

Концентрические волны

Моделировалась система уравнений (8) на клеточном множестве размерами 200х200 при $d=0,3, q=0,1$ и начальных концентрациях $u(0)=v(0)=q$ на всем моделируемом пространстве, кроме трех точек возбуждения (рис.3). КА-диффузия выполнялась двумерным алгоритмом поворота блоков, КН-реакция - по формулам (17). На рис. 3 показаны возникающие вокруг точек возбуждения концентрические волны.

Рис. 3: Концентрические волны, порождаемые уравнениями (8)
\begin{figure} \begin{center} \epsfxsize=12cm\ %%\epsfysize=12cm \epsfbox{lia... ...ненные кривые $u^\prime(j)$, b) затухающая вспышка} \end{center} \end{figure}

5. Заключение

Предложена дискретная математическая модель нелинейной пространственной динамики, обладающая свойствами мелкозернистого параллелизма. Вычислительные свойства модели обещают быть простыми и достаточно удобными для исследования качественных характеристик процессов в активных средах. Более подробные оценки вычислительных свойств метода (устойчивость к ошибкам округления, производительность, точность, распараллеливаемость) еще предстоит сделать.

Литература

1
Achasova S.,Bandman O., Markova V., Piskunov S. Parallel Substitution Algorithm/ Theory and Applications.- Singapore: World Scientific, 1994.-P.240.

2
Bandman O.L. Comparative Study of Cellular-Automata Diffusion Models // Lecture Notes in Computer Science. Vol.1662. 1999. Springer-Verlag, Berlin. - P.395-409.

3
Toffolli T. Cellular Automata as an Alternative to (rather than an Approximation of) Differetial Equations in Modeling Physics // Physica, 1984. Vol. 10D. - P.117-127.

4
Wolfram S. Cellular Automaton Fluids 1: Basic Theory // Journal of Statistical Physics. Vol.45. 1986. N 3/4. - P.471-525.

5
Бандман О.Л. Мелкозернистый параллелизм в математической физике // Программирование, 2001. N 4. - С.1-17.

6
Колебания и бегущие волны в химических системах. / Ред. Р.Филд, М.Бургер. - М.Мир, 1998. - 720 с.

7
Колмогоров А.Н., Петровский И.Г., Пискунов И.С. Исследование уравнений диффузии, соединенноq с возрастанием вещества, и его применение к одной биологической проблеме. - Бюл.МГУ, 1937. Т.1, сер.А, вып.Б. - 16 с.

8
Малинецкий Г.Г., Степанцов М.Е. Моделирование диффузионных процессов клеточными автоматами с окрестностью Марголуса // Журнал вычислительной математики и математической физики, 1998. Т.36.N 6. - C.1017-1021.

9
Нейроинформатика / Горбань А.Н., Дунин-Барковский В.Л., Кирдин А.Н.и др. - Новосибирск: Наука. Сибирское предприятие РАН, 1998. - 296 с.

10
Свирежев Ю.М. Нелинейные волны, диссипативные структуры и катастрофы в экологии. - М.: Наука, 1987.- 368 с.

Примечание

... сред 1
Работа поддержана грантом РФФИ 00-01-00026.
Ваши комментарии
[SBRAS]
[Головная страница]
[Конференции]
[СО РАН]

© 2001, Сибирское отделение Российской академии наук, Новосибирск
© 2001, Объединенный институт информатики СО РАН, Новосибирск
© 2001, Институт вычислительных технологий СО РАН, Новосибирск
© 2001, Институт систем информатики СО РАН, Новосибирск
© 2001, Институт математики СО РАН, Новосибирск
© 2001, Институт цитологии и генетики СО РАН, Новосибирск
© 2001, Институт вычислительной математики и математической геофизики СО РАН, Новосибирск
© 2001, Новосибирский государственный университет
Дата последней модификации Tuesday, 11-Sep-2001 16:54:34 NOVST