

Информационная система "Конференции"
Международная конференция молодых ученых по математическому моделированию и информационным технологиям
29-31 октября 2002 г., Новосибирск, Академгородок
Мацех А.М.
ИВТ СО РАН (Новосибирск)
Анализ алгоритмов вычисления сингулярных чисел и сингулярных
векторов несимметричных матриц по соответствующим матрицам в форме Голуба-Кахана.
Аннотация:
Сингулярные числа произвольной несимметричной матрицы являются еe
ортогональными инвариантами и совпадают с сингулярными числами
некоторой двухдиагональной матрицы, ортогонально подобной исходной.
Сингулярные числа произвольной двухдиагональной матрицы в свою
очередь совпадают с неотрицательными собственными значениями
симметричной трeхдиагональной матрицы в так называемой форме
Голуба-Кахана, имеющей нулевую главную диагональ и побочные
диагонали составленные из перемежевающихся элементов соответствующей
двухдиагональной матрицы. В работе исследуются вопросы адаптации алгоритмов решения
симметричных задач на собственные значения с гарантированной
точностью для определения сингулярных чисел и сингулярных векторов
несимметричных матриц по соответствующим матрицам в форме Голуба-Кахана.
Произвольная прямоугольная вещественная матрица
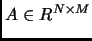 может быть преведена к
спектрально-эквивалентному двухдиагональному виду
некоторыми ортогональными преобразованиями
может быть преведена к
спектрально-эквивалентному двухдиагональному виду
некоторыми ортогональными преобразованиями
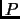 и
и 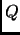 [Год97].
Ненулевая часть
[Год97].
Ненулевая часть  матрицы
матрицы 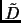 является квадратной
двухдиагональной матрицей размерности
является квадратной
двухдиагональной матрицей размерности
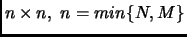 . Без потери общности можно предположить что матрица
. Без потери общности можно предположить что матрица  является
верхнедиагональной матрицей вида
причем элементы главной диагонали
является
верхнедиагональной матрицей вида
причем элементы главной диагонали
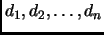 являются
собственными значениями матрицы
являются
собственными значениями матрицы  .
Произвольная квадратная вещественная матрица допускает сингулярное
разложение [Год97], и следовательно матрица
.
Произвольная квадратная вещественная матрица допускает сингулярное
разложение [Год97], и следовательно матрица  может быть представлена в виде
где
может быть представлена в виде
где 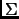 является диагональной матрицей вида
составленной из сингулярных чисел
является диагональной матрицей вида
составленной из сингулярных чисел
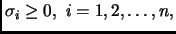 а ортогональные матрицы
а ортогональные матрицы 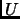 и
и 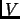 называются соответственно матрицами левых и
правых сингулярных векторов. Таким образом
сингулярное разложение исходной матрицы
называются соответственно матрицами левых и
правых сингулярных векторов. Таким образом
сингулярное разложение исходной матрицы 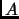 имеет вид
что означает что задача
об определении сингулярного разложения для матрицы
имеет вид
что означает что задача
об определении сингулярного разложения для матрицы 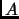 сводится к
задаче определения сингулярного разложения для двухдиагональной
матрицы
сводится к
задаче определения сингулярного разложения для двухдиагональной
матрицы  [ГАКК88], которая может быть получена к
примеру применением
цепочек ортогональных преобразований отражения если матрица
[ГАКК88], которая может быть получена к
примеру применением
цепочек ортогональных преобразований отражения если матрица 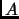 плотная, и методом Арнольди или несимметричным методом Ланцоша, если
матрица
плотная, и методом Арнольди или несимметричным методом Ланцоша, если
матрица 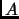 является разреженной матрицей с известной
структурой [GL96].
В этой работе мы не останавливаемся на деталях реализации
этих алгоритмов, концентрируя внимание на решении соответствующей
двухдиагональной задачи. Сингулярные числа этих задач совпадают с
точностью определяемой качеством ортогональных преобразований
является разреженной матрицей с известной
структурой [GL96].
В этой работе мы не останавливаемся на деталях реализации
этих алгоритмов, концентрируя внимание на решении соответствующей
двухдиагональной задачи. Сингулярные числа этих задач совпадают с
точностью определяемой качеством ортогональных преобразований 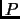 и
и
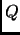 . В общем погрешность таких преобразованой должна быть величиной
порядка погрешности машинного представления единицы умноженной на
норму матрицы
. В общем погрешность таких преобразованой должна быть величиной
порядка погрешности машинного представления единицы умноженной на
норму матрицы 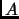 .
Применяя преобразования
.
Применяя преобразования 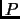 и
и 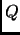 соответственно
к левым и правым сингулярным векторам матрицы
соответственно
к левым и правым сингулярным векторам матрицы  мы получаем
аппроксимацию сунгулярных векторов матрицы
мы получаем
аппроксимацию сунгулярных векторов матрицы 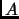 , погрешность которых
уже зависит не только от погрешностей двухдиагонализации,
но также и от точности определения сингулярного разложения матрицы
, погрешность которых
уже зависит не только от погрешностей двухдиагонализации,
но также и от точности определения сингулярного разложения матрицы
 .
Сингулярные числа произвольной матрицы могут быть
определены как неотрицательные собственные значения соответствующей
формы Жордана-Вейланда [Ste93]. Форма Жордана-Вейланда
для двухдиагональной матрицы
.
Сингулярные числа произвольной матрицы могут быть
определены как неотрицательные собственные значения соответствующей
формы Жордана-Вейланда [Ste93]. Форма Жордана-Вейланда
для двухдиагональной матрицы  имеет вид
причем собственные значения
имеет вид
причем собственные значения
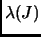 и сингулярные числа
и сингулярные числа
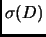 связяны следующим образом:
Ортогональными преобразованиями перестановок
связяны следующим образом:
Ортогональными преобразованиями перестановок 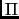 форма Жордана-Вейланда
форма Жордана-Вейланда
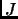 двухдиагональной матрицы
двухдиагональной матрицы  может быть приведена к
эквивалентной форме Голуба-Кахана [Fer98]
причем связь между собственными значениями и сингулярными числами сохраняется:
a собственный вектор
может быть приведена к
эквивалентной форме Голуба-Кахана [Fer98]
причем связь между собственными значениями и сингулярными числами сохраняется:
a собственный вектор
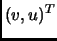 матрицы
матрицы 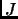 переводится преобразованием
переводится преобразованием 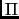 в вектор [ГАКК88]
Следовательно, решая частичную задачу на собственные значения
для матрицы
в вектор [ГАКК88]
Следовательно, решая частичную задачу на собственные значения
для матрицы 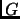 мы можем определить сингулярные числа и
соответствующие сингулярные векторы матрицы
мы можем определить сингулярные числа и
соответствующие сингулярные векторы матрицы  .
.
Вычислительная схема сингулярного разложения произвольной
вещественной матрицы 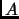 по соответствующей матрице Голуба-Кахана
может быть сформулирована в виде следующего алгоритма:
по соответствующей матрице Голуба-Кахана
может быть сформулирована в виде следующего алгоритма:
Остановимся подробнее на деталях машинной реализации описанной
схемы. Мы предполагаем что матрица 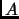 приводится к двухдиагональному
виду
приводится к двухдиагональному
виду  почти ортогональными преобразованиями с погрешностью не намного
превышающей
почти ортогональными преобразованиями с погрешностью не намного
превышающей
 , где
, где 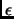 представляет собой
погрешность округления чисел с вещественной точкой на используемой
архитектуре. Матрица
представляет собой
погрешность округления чисел с вещественной точкой на используемой
архитектуре. Матрица  в явном виде не строятся - элементы
в явном виде не строятся - элементы  хранятся в виде вектора
хранятся в виде вектора
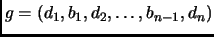 составленного из перемежевающихся элементов главной и побочной
диагоналей матрицы
составленного из перемежевающихся элементов главной и побочной
диагоналей матрицы  . Вектор
. Вектор 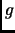 соответствует побочной диагонали
матрицы Голуба-Кахана
соответствует побочной диагонали
матрицы Голуба-Кахана 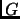 . Сингулярные числа
матрицы
. Сингулярные числа
матрицы  вычисляются методом бисекций основанном на применении закона инерции Сильвестра
для подсчета неположительных собственных значений матрицы
вычисляются методом бисекций основанном на применении закона инерции Сильвестра
для подсчета неположительных собственных значений матрицы
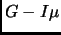 . Точность при подсчете собственных
значений имеет критическое значение при решении данной задачи, поскольку даже малые
погрешности при вычислении сингулярных (собственных) чисел влекут за
собой значительные погрешности при определении сингулярных
(собственных) векторов. Метод бисекций является наиболее
робастным среди методов определения собственных чисел симметричных
матриц, и при аккуратном подсчете смен знаков позволяет
вычислять интервалы содержащие собственные числа рассматриваемой
матрицы с гарантированой точностью. Соответствующие собственные
векторы матрицы
. Точность при подсчете собственных
значений имеет критическое значение при решении данной задачи, поскольку даже малые
погрешности при вычислении сингулярных (собственных) чисел влекут за
собой значительные погрешности при определении сингулярных
(собственных) векторов. Метод бисекций является наиболее
робастным среди методов определения собственных чисел симметричных
матриц, и при аккуратном подсчете смен знаков позволяет
вычислять интервалы содержащие собственные числа рассматриваемой
матрицы с гарантированой точностью. Соответствующие собственные
векторы матрицы 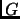 могут быть вычислены методом Обратной
Итерации [ABB+95], методом Годунова, основанном на применении составных
последовательностей Штурма [ГАКК88], или методом
Годунова с итерационным уточнением [МШ01].
могут быть вычислены методом Обратной
Итерации [ABB+95], методом Годунова, основанном на применении составных
последовательностей Штурма [ГАКК88], или методом
Годунова с итерационным уточнением [МШ01].
Традиционно подсчет неотрицательных собственных чисел основывался на подсчете
неположительных элементов в последовательности Штурма матрицы 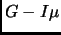 [Год97]. Однако,
поскольку последовательности Штурма вычисляются по главным минорам матрицы
[Год97]. Однако,
поскольку последовательности Штурма вычисляются по главным минорам матрицы 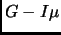 , среди элементов последовательности могут появляться числа
непредставимые в машинной арифметике. Для избежания таких ситуаций при
подсчете собственных чисел по последовательностям Штурма требуется
вносить малые погрешности в элементы матрицы
, среди элементов последовательности могут появляться числа
непредставимые в машинной арифметике. Для избежания таких ситуаций при
подсчете собственных чисел по последовательностям Штурма требуется
вносить малые погрешности в элементы матрицы
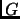 [ГАКК88], имеющей нулевую главную
диагональ. Однако внесение погрешностей в элементы
главной диагонали нежелательно. Современная версия метода
бисекций основывается на применении закона инерции
Сильвестра, согласно которому инерция конгруэнтных
матриц остается неизменной [GL96]. Это означает что
число отрицательных, положительных и нулевых собственных значений
симметричной матрицы
[ГАКК88], имеющей нулевую главную
диагональ. Однако внесение погрешностей в элементы
главной диагонали нежелательно. Современная версия метода
бисекций основывается на применении закона инерции
Сильвестра, согласно которому инерция конгруэнтных
матриц остается неизменной [GL96]. Это означает что
число отрицательных, положительных и нулевых собственных значений
симметричной матрицы
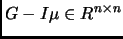 и конгруэнтной
ей матрицы
и конгруэнтной
ей матрицы
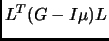 , где матрица
, где матрица
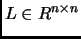 невырожденная,
совпадает. Диагональная матрица
невырожденная,
совпадает. Диагональная матрица
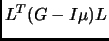 может быть получена при
помощи Гауссова исключения, причем элементы
может быть получена при
помощи Гауссова исключения, причем элементы 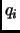 главной
диагонали матрицы
главной
диагонали матрицы
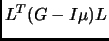 имеют вид [Fer98]:
В IEEE-арифметике, при правильном масштабировании матрицы
имеют вид [Fer98]:
В IEEE-арифметике, при правильном масштабировании матрицы  для
избежания ситуаций деления на ноль и бесконечность, функция
для
избежания ситуаций деления на ноль и бесконечность, функция
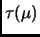 , равная числу отрицательных
элементов
, равная числу отрицательных
элементов 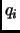 , является монотонной функцией, и следовательно
пригодна для подсчета отрицательных собственных значений матрицы
, является монотонной функцией, и следовательно
пригодна для подсчета отрицательных собственных значений матрицы
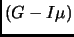 [Fer98], причем элементы матрицы
[Fer98], причем элементы матрицы  масштабируются так,
чтобы удовлетворялось условие
где
масштабируются так,
чтобы удовлетворялось условие
где 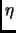 представляет собой минимальное положительное машинное
число представимое в IEEE-арифметике,
представляет собой минимальное положительное машинное
число представимое в IEEE-арифметике, 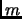 является максимальным
целым машинным числом, а
является максимальным
целым машинным числом, а 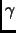 определяется таким образом,
что
определяется таким образом,
что
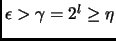 для
некоторого целого числа
для
некоторого целого числа 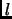 . Посколку
. Посколку 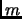 является целым числом,
параметр масштабирования
является целым числом,
параметр масштабирования 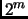 не вносит погрешностей в элементы
матрицы
не вносит погрешностей в элементы
матрицы  . Требуя дополнительно, чтобы
. Требуя дополнительно, чтобы
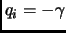 в случае
если
в случае
если
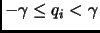 , мы получаем алгоритм для подсчета
отрицательных элементов
, мы получаем алгоритм для подсчета
отрицательных элементов  матрицы
матрицы
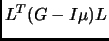 :
:
Сингулярные числа матрицы  ищутся на интерале
ищутся на интерале ![$ [X, Y]$](img76.png) ,
определяемом свойствами сингулярных чисел трехдиагональных матриц
следующим образом [ГАКК88]:
причем
Положив
,
определяемом свойствами сингулярных чисел трехдиагональных матриц
следующим образом [ГАКК88]:
причем
Положив
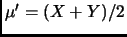 , и вычислив инерцию
матрицы
, и вычислив инерцию
матрицы 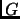 , можно выяснить число собственных
значений, меньших
, можно выяснить число собственных
значений, меньших 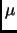 , а значит решить какому из
полуинтервалов
, а значит решить какому из
полуинтервалов
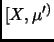 , или
, или
![$ (\mu^{\prime}, Y]$](img82.png) ,
принадлежит
,
принадлежит 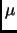 . Процесс последовательного деления
интервалов, окружающих
. Процесс последовательного деления
интервалов, окружающих 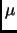 , продолжается до пор, пока
в результате сближения границ величина интервала
, продолжается до пор, пока
в результате сближения границ величина интервала
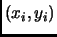 ,
содержащего
,
содержащего 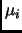 , не сравнима с
, не сравнима с
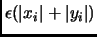 .
.
Поскольку задача отыскания сингулярных векторов двухдиагональной
матрицы  сводится к задаче определения собственных векторов
симметричной трехдиагональной матрицы
сводится к задаче определения собственных векторов
симметричной трехдиагональной матрицы 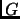 , мы исследовали возможность
преименения методов Обратной Итерации [ABB+95], метода
Годунова [ГАКК88], и метода Годунова с итерационным
уточнением [МШ01] для решения данной задачи. Метод
Годунова имеет сложность
, мы исследовали возможность
преименения методов Обратной Итерации [ABB+95], метода
Годунова [ГАКК88], и метода Годунова с итерационным
уточнением [МШ01] для решения данной задачи. Метод
Годунова имеет сложность 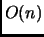 операций с вещественной точкой для
определения собственного вектора, но требует внесения погрешностей в
элемены главной диагонали матрицы
операций с вещественной точкой для
определения собственного вектора, но требует внесения погрешностей в
элемены главной диагонали матрицы  , что приводит к потере
точности при вычислениях. Одновременно метод Годунова генерирует
почти коллинеарные векторы, соответствующие близким собственным
значениям, в то время как метод Обратной Итерации включает в себя
шаг выборочной реортогонализации. В большенстве экспериментов метод обратной
итерации доставляет меньшие погрешности, чем метод Годунова,
являющийся прямым методом по своей природе, и требующим внесения
погрешностей в нулевые диагональные элементы. Однако метод Обратной
Итерации является итерационной процедурой требующей вплоть до
, что приводит к потере
точности при вычислениях. Одновременно метод Годунова генерирует
почти коллинеарные векторы, соответствующие близким собственным
значениям, в то время как метод Обратной Итерации включает в себя
шаг выборочной реортогонализации. В большенстве экспериментов метод обратной
итерации доставляет меньшие погрешности, чем метод Годунова,
являющийся прямым методом по своей природе, и требующим внесения
погрешностей в нулевые диагональные элементы. Однако метод Обратной
Итерации является итерационной процедурой требующей вплоть до
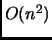 действий с вещественной точкой для вычисления собственного
вектора. В отличии от алгоритма Годунова в методе Обратной
Итерации сходимость к решению не гарантирована, поскольку начальный
вектор может не иметь нетривиальной компоненты в направлении
искомого решения.
действий с вещественной точкой для вычисления собственного
вектора. В отличии от алгоритма Годунова в методе Обратной
Итерации сходимость к решению не гарантирована, поскольку начальный
вектор может не иметь нетривиальной компоненты в направлении
искомого решения.
Альтернативным подходом к решению данной
задачи является разработанный нами гибридный алгоритм Годунова с
итерационным уточнением, или метод Годунова-Обратной
Итерации [ГАКК88]. Идея метода заключается в том,
чтобы использовать векторы расчитанные методом Годунова с
гарантированной точностью как черезвычайно точные начальные векторы
в методе Обратной Итерации, имеющие нетривиальную компоненту в
направлении искомого решения. Как правило одного-двух шагов обратной
итерации оказывается достаточным для достижения требуемой точности,
в то время как, к примеру метод Обратной Итерации, реализованный
в пакете LAPACK в виде процедуры STEIN [ABB+95] требует
трех-пяти шагов. Одновременно, на шаге итерационного уточнения мы
реортогонализуем векторы вычисленные методом Годунова, получая таким
образом результаты сравнимые или даже превосходящие результаты
обратной итерации, требующей большего числа шагов, и не всегда
сходящегося. Формально метод Годунова-Обратной Итерации может быть
описан в виде следующего алгоритма:
Нами разработан пакет программ реализующий описанные алгоритмы
сингулярного разложения в двойной точности на языке C в IEEE
арифметике. В качестве иллюстрации работы этого пакета мы приводим
примеры расчета сингулярных чисел и сингулярных векторов нескольких
двухдиагональные матриц (примеры 1- 4), описанных
в монографии С. К. Годунаова et. al [ГАКК88]. Расчеты
проводились в операционной системе Linux, с использованием
компилятора GNU C на персоональном компьютере имеющем следующие
параметры: i686 Intel(R) Xeon(TM) CPU 1500MHz.
В таблице 1 представлены погрешности расчета машинных
интервалов
![$ [x_i, y_i]$](img122.png) содержащих сингулярные
числа
содержащих сингулярные
числа 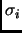 с гарантированной точностью, а также максимальные
и минимальные сингулярные числа рассматриваемых тестовых матриц. Сингулярные числа
с гарантированной точностью, а также максимальные
и минимальные сингулярные числа рассматриваемых тестовых матриц. Сингулярные числа
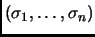 были расчитаны методом бисекций, основанном на
использовании инерции Сильвестра.
В таблице 2 представлены оценки вычислительной
погрешности сингулярного разложения
были расчитаны методом бисекций, основанном на
использовании инерции Сильвестра.
В таблице 2 представлены оценки вычислительной
погрешности сингулярного разложения
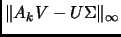 тестовых матриц, а также оценки ортогональности сингулярных
векторов
тестовых матриц, а также оценки ортогональности сингулярных
векторов  тестовых матриц, расчитанных в соответствии с
методом Годунова с Итерационным Уточнением с использованием в
качестве сдвига правых границ
тестовых матриц, расчитанных в соответствии с
методом Годунова с Итерационным Уточнением с использованием в
качестве сдвига правых границ 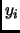 интервалов
интервалов
![$ [x_i, y_i]$](img122.png) , содержащих соответствующие
собственные значения. В таблице 3 представлены алалогичные характеристики
сингулярных векторов, расчитанных методом обратной итерации по
алгоритму STEIN из пакета LAPACK [ABB+95] с использованием в
качестве сдвига правых границ
, содержащих соответствующие
собственные значения. В таблице 3 представлены алалогичные характеристики
сингулярных векторов, расчитанных методом обратной итерации по
алгоритму STEIN из пакета LAPACK [ABB+95] с использованием в
качестве сдвига правых границ 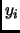 интервалов
интервалов
![$ [x_i, y_i]$](img122.png) , содержащих соответствующие
собственные значения, и наконец в таблице
4 представлены соответствующие характеристики
сингулярных векторов расчитанных методом Годунова.
Сравнивая таблицы 2- 4 мы убеждаемся что метод
Годунова с Итерационным Уточнением значительно улучшает качество
сингулярных (собственных) векторов, расчитанных методом
Годунова. Используя меньшее число итераций чем метод Обратной
Итерации, метод Годунова с Итерационным Уточнением позволяет
расчитывать сингулярные (собственные) векторы практически с такой же
точностью.
, содержащих соответствующие
собственные значения, и наконец в таблице
4 представлены соответствующие характеристики
сингулярных векторов расчитанных методом Годунова.
Сравнивая таблицы 2- 4 мы убеждаемся что метод
Годунова с Итерационным Уточнением значительно улучшает качество
сингулярных (собственных) векторов, расчитанных методом
Годунова. Используя меньшее число итераций чем метод Обратной
Итерации, метод Годунова с Итерационным Уточнением позволяет
расчитывать сингулярные (собственные) векторы практически с такой же
точностью.
Пример 1
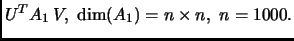
Сингуярные числа рассматриваемой матрицы были расчитаны с
гарантированной точностью
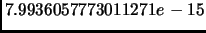
.
Результаты аналогичного расчета сингулярных чисел в пакете Matlab
согласовались с нашими результатами с максимальной погрешностью равной
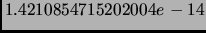
. Максимальная погрешность сингулярного
разложения вычисленного методом Годунова с Итерационным Уточнением
равна

.
Пример 2
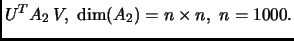
Сингуярные числа рассматриваемой матрицы были расчитаны с
гарантированной точностью
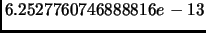
.
Результаты аналогичного расчета сингулярных чисел в пакете Matlab согласовались с
нашими результатами с максимальной погрешностью равной
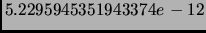
. Максимальная погрешность сингулярного
разложения вычисленного методом Годунова с Итерационным Уточнением
равна
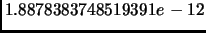
.
Пример 3
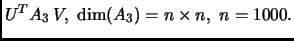
Сингулярные
числа матрицы
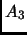
являются корнями полиномов Чебышева
2-го рода, и выражаются формулой:
Сингуярные числа рассматриваемой матрицы были расчитаны с
гарантированной точностью

, причем
максимальное отклонение вычисленных нами сингулярных чисел от
соответствующих значений расчитанных по аналитической формуле
равнялось точно
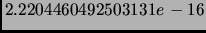
-- т.е. машинной
погрешности представления единицы в IEEE арифметике с
двойной точностью. Результаты аналогичного расчета сингулярных чисел
в пакете Matlab согласовались с
аналитическими результатами с максимальной погрешностью равной лишь
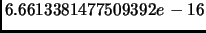
. Максимальная погрешность сингулярного
разложения вычисленного методом Годунова с Итерационным Уточнением
равна

.
Пример 4
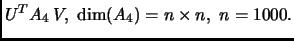
Элементы гавной и побочной
диагоналей этой матрицы вычисляются по формулам:
Сингулярные числа матрицы
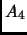
являются
ортонормированными полиномами Лежандра и были расчитаны с
гарантированной точностью
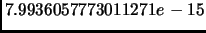
.
Результаты аналогичного расчета сингулярных чисел в пакете Matlab
согласовались с нашими результатами с максимальной погрешностью
равной
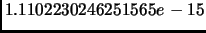
. Максимальная погрешность сингулярного
разложения вычисленного методом Годунова с Итерационным Уточнением
равна
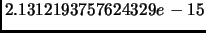
.
Таблица:
Погрешность определения сингулярных чисел, и максимальные
и минимальные сингулярные числа матриц из примеров
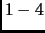 .
.
| |
Таблица:
Вычислительная погрешность сингулярного разложения и
характеристика ортогональности левых и правых сингулярных векторов
матриц из примеров
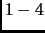 вычисленных методом Годунова с Итерационным Уточнением.
вычисленных методом Годунова с Итерационным Уточнением.
| |
Таблица:
Вычислительная погрешность сингулярного разложения и
характеристика ортогональности левых и правых сингулярных векторов
матриц из примеров
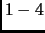 вычисленных методом
Обратной Итерации.
вычисленных методом
Обратной Итерации.
| |
Таблица:
Вычислительная погрешность сингулярного разложения и
характеристика ортогональности левых и правых сингулярных векторов
матриц из примеров
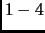 вычисленных методом Годунова.
вычисленных методом Годунова.
| |
-
- ГАКК88
-
С. К. Годунов, А. Г. Антонов, О. П. Кирилюк, В. И.
Костин.
Гарантированная точность решения систем линейных уравнений в
евклидовых пространствах.
Наука, Новосибирск, 1988.
- Год97
-
С. К. Годунов.
Современные аспекты линейной алгебры.
Научная книга, Новосибирск, 1997.
- МШ01
-
А. М. Мацех, Э. П. Шурина.
Решение трехдиагональной симметричной проблемы собственных значений с
гарантированной точностью за О(n**2) операций.
Современные проблемы прикладной математики и механики: теория,
эксперимент и практика. Академгородок, Новосибирск, Россия, 24-29 Июня
2001.
- ABB+95
-
E. Anderson, Z. Bai, C. Bischof, J. Demmel, J. Dongarra, J. Du Croz,
A. Greenbaum, S. Hammarling, A McKenney, S. Ostrouchov, D. Sorensen.
LAPACK Users' Guide.
SIAM, Philadelphia, second edition, 1995.
- Fer98
-
K. V. Fernando.
Accurately counting singular values of bidiagonal matrices and
eigenvalues of skew-symmetric tridiagonal matrices.
SIAM Journal on Matrix Analysis and Applications,
20(2):373-399, 1998.
- GL96
-
Gene H. Golub, Charles F. Van Loan.
Matrix Computations.
The Johns Hopkins University Press, third edition, 1996.
- Ste93
-
G. W. Stewart.
On the early history of the singular value decomposition.
SIAM Review, 35(4):551-566, 1993.
Анализ алгоритмов вычисления сингулярных чисел и сингулярных
векторов несимметричных матриц по соответствующим матрицам в форме Голуба-Кахана.
This document was generated using the
LaTeX2HTML translator Version 2K.1beta (1.47)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -no_math -html_version 3.2 -split 0 ysci_2002.tex ysci_2002.html
The translation was initiated by Anna Matsekh on 2002-10-23
Anna Matsekh
2002-10-23


![$\displaystyle D = \left[\begin{array}{ccccc}
d_1 & b_1 & & & \\
& d_2 & b_2 &...
... & \ddots & \\
& & & d_{n-1} & b_{n-1} \\
& & & & d_n
\end{array} \right],
$](img9.png)
![$\displaystyle \Sigma = \left[\begin{array}{ccccc}
\sigma_1 & & & \\
& \sigma_2 & & \\
& &\ddots& & \\
& & & & \sigma_{n} \\
\end{array} \right]
$](img13.png)
![$\displaystyle J =
\left[
\begin{array}{cc} 0 & D \\ D^* & 0 \end{array}
\right]
$](img19.png)
![$\displaystyle G = \left[\begin{array}{cccccc}
0 & d_1 & & & & \\
d_1 & 0 & b_...
...ots & & \\
& & & b_{n-1} & 0 & d_n \\
& & & & d_n & 0
\end{array} \right]
$](img25.png)
![$\displaystyle \left[\begin{array}{c}
u^1 \\ v^1 \\ u^2 \\ v^2\\ \vdots \\ ...
...\end{array} \right] = \Pi
\left[\begin{array}{c}
v \\ u
\end{array} \right].
$](img28.png)
![]() по соответствующей матрице Голуба-Кахана
может быть сформулирована в виде следующего алгоритма:
по соответствующей матрице Голуба-Кахана
может быть сформулирована в виде следующего алгоритма:
![]() содержащих сингулярные
числа
содержащих сингулярные
числа ![]() с гарантированной точностью, а также максимальные
и минимальные сингулярные числа рассматриваемых тестовых матриц. Сингулярные числа
с гарантированной точностью, а также максимальные
и минимальные сингулярные числа рассматриваемых тестовых матриц. Сингулярные числа
![]() были расчитаны методом бисекций, основанном на
использовании инерции Сильвестра.
В таблице 2 представлены оценки вычислительной
погрешности сингулярного разложения
были расчитаны методом бисекций, основанном на
использовании инерции Сильвестра.
В таблице 2 представлены оценки вычислительной
погрешности сингулярного разложения
![]() тестовых матриц, а также оценки ортогональности сингулярных
векторов
тестовых матриц, а также оценки ортогональности сингулярных
векторов ![]() тестовых матриц, расчитанных в соответствии с
методом Годунова с Итерационным Уточнением с использованием в
качестве сдвига правых границ
тестовых матриц, расчитанных в соответствии с
методом Годунова с Итерационным Уточнением с использованием в
качестве сдвига правых границ ![]() интервалов
интервалов
![]() , содержащих соответствующие
собственные значения. В таблице 3 представлены алалогичные характеристики
сингулярных векторов, расчитанных методом обратной итерации по
алгоритму STEIN из пакета LAPACK [ABB+95] с использованием в
качестве сдвига правых границ
, содержащих соответствующие
собственные значения. В таблице 3 представлены алалогичные характеристики
сингулярных векторов, расчитанных методом обратной итерации по
алгоритму STEIN из пакета LAPACK [ABB+95] с использованием в
качестве сдвига правых границ ![]() интервалов
интервалов
![]() , содержащих соответствующие
собственные значения, и наконец в таблице
4 представлены соответствующие характеристики
сингулярных векторов расчитанных методом Годунова.
Сравнивая таблицы 2- 4 мы убеждаемся что метод
Годунова с Итерационным Уточнением значительно улучшает качество
сингулярных (собственных) векторов, расчитанных методом
Годунова. Используя меньшее число итераций чем метод Обратной
Итерации, метод Годунова с Итерационным Уточнением позволяет
расчитывать сингулярные (собственные) векторы практически с такой же
точностью.
, содержащих соответствующие
собственные значения, и наконец в таблице
4 представлены соответствующие характеристики
сингулярных векторов расчитанных методом Годунова.
Сравнивая таблицы 2- 4 мы убеждаемся что метод
Годунова с Итерационным Уточнением значительно улучшает качество
сингулярных (собственных) векторов, расчитанных методом
Годунова. Используя меньшее число итераций чем метод Обратной
Итерации, метод Годунова с Итерационным Уточнением позволяет
расчитывать сингулярные (собственные) векторы практически с такой же
точностью.
![% latex2html id marker 2859
$\displaystyle A_{\ref{ex_a}} = \left[\begin{array}{...
...\
& &\ddots & \ddots & \\
& & & 1 & 10 \\
& & & & 1
\end{array} \right],
$](img129.png)
![% latex2html id marker 2870
$\displaystyle A_{\ref{ex_b}} = \left[\begin{array}{...
...\ddots & \ddots & \\
& & & 0.01 & 900 \\
& & & & 0.01
\end{array} \right],
$](img134.png)
![% latex2html id marker 2881
$\displaystyle A_{\ref{ex_c}} = \left[\begin{array}{...
... &\ddots & \ddots & \\
& & & 0.5 & 0.5 \\
& & & & 0.5
\end{array} \right],
$](img139.png)
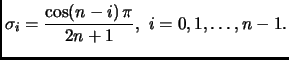
![% latex2html id marker 2898
$\displaystyle A_{\ref{ex_d}} = \left[\begin{array}{...
... & \ddots & \\
& & & d_{n-1} & b_{n-1} \\
& & & & d_n
\end{array} \right],
$](img147.png)