

Информационная система "Конференции"
Международная конференция молодых ученых по математическому моделированию и информационным технологиям
29-31 октября 2002 г., Новосибирск, Академгородок
Стыврин А.В.
Новосибирский государственный технический университет
Анализ решения задач распространения поверхностных волн на воде методом ММКО на
неструктурированных сетках
Аннотация
В работе описана новая вычислительная схема для вычисления распространения
волн на свободной поверхности воды, использующая модель мелкой воды.
Дискретизация по времени осуществляется с помощью явно-неявной схемы.
Модифицированный метод конечных объемов используется для аппроксимации
задачи по пространству. Предложенная схема использует для расчета нерегулярную
треугольную сетку. Приведены сравнения влияния качества двух сеток, построенных
с помощью метода фронтальной триангуляции, на устойчивость предложенного метода.
Математическая модель
Для моделирования процессов распространения поверхностных волн на воде с учетом
эффектов нелинейности, традиционно используется классическая модель мелкой воды [1]:

 ,
,
где  -полная глубина;
-полная глубина;  -глубина под
невозмущенным слоем жидкости;
-глубина под
невозмущенным слоем жидкости;  -возвышение свободной
поверхности над невозмущенным слоем жидкости;
-возвышение свободной
поверхности над невозмущенным слоем жидкости; 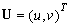 -осреднённый
по глубине вектор скоростей;
-осреднённый
по глубине вектор скоростей;  -компоненты осредненного
вектора скоростей по
-компоненты осредненного
вектора скоростей по  -,
-, -направлениям
соответственно;
-направлениям
соответственно;  -ускорение свободного падения.
-ускорение свободного падения.
Здесь и в дальнейшем будем придерживаться идеологии, предложенной в [8].
Поиск решения этой системы будем производить в гипервекторе:
 ,
где
,
где  ,
,  .
.
Граничные условия
Для замыкания математической модели, необходимо определить краевые условия. В
данной работе мы остановимся на двух видах краевых условий, моделирующих
отражение от границы и прохождение волны через границу без взаимодействия.
Дискретизация по времени
Для дискретизации по времени будем использовать явно-неявную схему с параметром
релаксации  :
:

При значении  предложенная схема соответствует явной схеме,
стандартная неявная схема может быть получена при значении
предложенная схема соответствует явной схеме,
стандартная неявная схема может быть получена при значении  .
Значение параметра
.
Значение параметра  соответствует неявной схеме Кранка-
Николсон. Экспериментально было получено значение параметра
соответствует неявной схеме Кранка-
Николсон. Экспериментально было получено значение параметра  , при котором предложенная схема работает наилучшим образом.
, при котором предложенная схема работает наилучшим образом.
Пространственная аппроксимация
Пространственная аппроксимация системы уравнения мелкой воды выполняется с
помощью модифицированного метода конечных объемов (ММКО). Следуя
конечнообъемной идеологии, домножая систему уравнений скалярно на тестовые
кусочно-постоянные функции и, затем, применяя формулу интегрирования по частям,
окончательно можно записать:

Для аппроксимации уравнения неразрывности используются линейные базисные
функции, для уравнения движения применены квадратичные базисные функции.
Построение такого метода приводит к удовлетворению условий ЛББ для совместной
аппроксимации, что гарантирует невырожденность решения [5, 6].
Использование треугольной нерегулярной сетки дает возможность достаточно
точного описания расчетной области, что играет немалую роль для получения
достоверного решения для задач рассматриваемого класса. Таким образом,
аппроксимация уравнения неразрывности происходит на базовой треугольной сетке,
а аппроксимация уравнения движения ( на сетке с дополнительными узлами,
построенными на серединах ребер каждого треугольника.
Дискретный аналог
В результате применения ММКО к системе уравнений мелкой воды, может быть
получен дискретный аналог, который имеет вид  , где вектор
неизвестных
, где вектор
неизвестных  , матрица
, матрица  имеет блочную
структуру; вектор правой части
имеет блочную
структуру; вектор правой части  имеет структуру,
соответствующую блочной структуре матрицы
имеет структуру,
соответствующую блочной структуре матрицы  . Размерность
этой матрицы равна сумме значений числа узлов в базовой сетке и удвоенного
числа узлов дополнительной сетки. Очевидно, что матрица
. Размерность
этой матрицы равна сумме значений числа узлов в базовой сетке и удвоенного
числа узлов дополнительной сетки. Очевидно, что матрица  ,
в результате предложенной аппроксимации, является слабо заполненной,
несимметричной, однако имеет симметричный портрет. Поэтому для хранения этой
разреженной матрицы используется разреженный строчный формат [9], что позволяет
существенным образом сократить затраты на память. Для решения системы линейных
алгебраических уравнений (СЛАУ) используется итерационный метод
стабилизированных бисопряженных градиентов BiCGStab [9].
,
в результате предложенной аппроксимации, является слабо заполненной,
несимметричной, однако имеет симметричный портрет. Поэтому для хранения этой
разреженной матрицы используется разреженный строчный формат [9], что позволяет
существенным образом сократить затраты на память. Для решения системы линейных
алгебраических уравнений (СЛАУ) используется итерационный метод
стабилизированных бисопряженных градиентов BiCGStab [9].
Результаты моделирования
В качестве тестовой задачи рассмотрим задачу взаимодействия уединенной
синусоидальной волны с цилиндрическим островом. Расчетная область представляет
собой прямоугольник  с ровным дном
с ровным дном  ,
цилиндрический остров радиуса
,
цилиндрический остров радиуса  расположен в начале
координат. На горизонтальных границах расчетной области и на границе
острова заданы отражающие граничные условия, на вертикальных границах-заданы
открытые граничные условия.
расположен в начале
координат. На горизонтальных границах расчетной области и на границе
острова заданы отражающие граничные условия, на вертикальных границах-заданы
открытые граничные условия.
В начальный момент времени  волна с амплитудой
волна с амплитудой
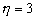 и длиной 10 расположена на позиции
и длиной 10 расположена на позиции  .
После этого она распадается на две уединенных волны, двигающихся в
противоположных направлениях.
.
После этого она распадается на две уединенных волны, двигающихся в
противоположных направлениях.
Построим треугольную сетку для решения этой задачи, используя алгоритм
фронтальной триангуляции. Эта сетка содержит 2319 узлов и 4437 элементов
(рис. 1).

рис. 1
Размерность матрицы СЛАУ, полученной при аппроксимации ММКО системы уравнений
мелкой воды на сетке, приведенной на рисунке 1, равна 20469. На рисунке 2
приведено начальное расположение волны в расчетной области.

рис. 2 Момент времени 
В дальнейшем, для моделирования поведения волновой поверхности в расчетной
области, используется описанный выше метод. Однако почти на первых же его
шагах по времени решение "разваливается", как можно увидеть на рисунке 3.
Это означает, что в характерных местах на треугольной сетке при решении
появляются нефизичные максимумы в численном решении, которые при дальнейшем
счете неограниченно растут. Детальное рассмотрение сетки в местах появления
выбросов решения, показывает, что треугольные элементы как раз в этом месте
меняют свой характерный размер, либо становятся слишком отличающимися по
конфигурации от соседних элементов разбиения (см. рисунок 4).

рис. 3 Момент времени 

рис. 4
Перестроим сетку, в которой дефекты построения, приведенные на рисунке 4,
отсутствуют. Новая сетка имеет 2406 узлов и 4596 элементов (см. рисунок 5).

рис. 5
Размерность матрицы СЛАУ, полученной при аппроксимации ММКО системы уравнений
мелкой воды на сетке, приведенной на рисунке 5, равна 21222. На этой сетке
волна взаимодействует с островом и беспрепятственно выходит за пределы
расчетной области через открытые границы. Эволюция волновой поверхности
показана на рисунках 6-8.

рис. 6 Момент времени 
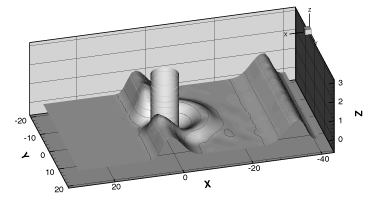
рис. 7 Момент времени 

рис. 8 Момент времени 
На рисунках 9 и 10 приведены портреты матриц, получающихся при аппроксимации
на первой и второй сетках соответственно. Портрет матрицы СЛАУ, соответствующий
сетке на рисунке 1, является более "размазанным", что помимо прочего ухудшает
сходимость итерационного метода решения. Портрет матрицы СЛАУ, соответствующий
сетке на рисунке 5, является более компактным, что приводит к значительному
улучшению сходимости итерационной процедуры, обеспечивающей сохранение
физичности решения (см. рисунки 6 - 8).

рис. 9

рис. 10
Заключение
Использование сетки для моделирования тестовой задачи, обладающей
геометрическими погрешностями, типа разномасштабных треугольников или вытянутых
треугольников, приводит к неустойчивости предложенного алгоритма. Эта проблема
решается лишь с помощью перестроения "плохой" сетки для устранения этих
погрешностей.
Таким образом, важной задачей для успешного моделирования задач волновой
гидродинамики, наряду с эффективными методами аппроксимации и методами решения
СЛАУ, является построения качественной сетки, описывающую расчетную область.
Такое требование к сеткам появляется вследствие того, что наряду со скалярным
уравнением неразрывности, также происходит расчет векторных уравнений движения.
Литература
- D. R. Lynch, W. G. Gray, A Wave Equation Model For Finite Element Tidal Computations, Computers and Fluids v. 7, 207-228 (1979)
- D. Ambrosi, L. Quartapelle, A Taylor-Galerkin Method for Simulating Nonlinear Dispersive Water Waves, Journal of Computational Physics 146, 546-569 (1998)
- J. E. Romate, Absorbing Boundary Conditions for Free Surface Waves, Journal of Computational Physics 99, 135-145 (1992)
- Э. П. Шурина, О. П. Солоненко, Т. В. Войтович, Новая технология метода конечных объемов на симплициальных сетках для задач конвективно-диффузионного типа, препринт №8-99, СО РАН ИТПМ
- О. А. Ладыженская, Математические вопросы динамики вязкой несжимаемой жидкости, М. Гос. изд-во ф.-м. лит., 1961
- F. Babushka, Error Bounds for Finite Element Methods, Numer. Math., v. 16, 322-333 (1971)
- M. H. T. Chen, Tsunami Propagation and Response to Coastal Areas, HIG-73-15
- A. V. Stywrin, E. P. Shurina, L. B. Chubarov, The Feature of FVM/FEM-Approach for Modeling Surface Waves on Water, Proceeding of International Conferences on Computational Mathematics, 711-716, Novosibirsk 2002
- J. Saad, Iterative Methods for Sparse Linear Systems, PWS Publishing Company, 1996

 ,
,



 ,
,
 -полная глубина;
-полная глубина;  -глубина под
невозмущенным слоем жидкости;
-глубина под
невозмущенным слоем жидкости;  -возвышение свободной
поверхности над невозмущенным слоем жидкости;
-возвышение свободной
поверхности над невозмущенным слоем жидкости; 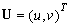 -осреднённый
по глубине вектор скоростей;
-осреднённый
по глубине вектор скоростей;  -компоненты осредненного
вектора скоростей по
-компоненты осредненного
вектора скоростей по  -,
-, -направлениям
соответственно;
-направлениям
соответственно;  -ускорение свободного падения.
-ускорение свободного падения.
 ,
,
 ,
,  .
.
 должны выполняться условия [2]:
должны выполняться условия [2]:  ,
,  ,
,
 -вектор внешней нормали к границе
-вектор внешней нормали к границе  .
.
 [3], описываются
следующими выражениями:
[3], описываются
следующими выражениями:  ,
, 
 -характерная скорость распространения волн на воде
(обычно
-характерная скорость распространения волн на воде
(обычно  ),
),  -вектор внешней нормали
к границе
-вектор внешней нормали
к границе  .
.
 :
:

 предложенная схема соответствует явной схеме,
стандартная неявная схема может быть получена при значении
предложенная схема соответствует явной схеме,
стандартная неявная схема может быть получена при значении  .
Значение параметра
.
Значение параметра  соответствует неявной схеме Кранка-
Николсон. Экспериментально было получено значение параметра
соответствует неявной схеме Кранка-
Николсон. Экспериментально было получено значение параметра  , при котором предложенная схема работает наилучшим образом.
, при котором предложенная схема работает наилучшим образом.

 , где вектор
неизвестных
, где вектор
неизвестных  , матрица
, матрица  имеет блочную
структуру; вектор правой части
имеет блочную
структуру; вектор правой части  имеет структуру,
соответствующую блочной структуре матрицы
имеет структуру,
соответствующую блочной структуре матрицы  . Размерность
этой матрицы равна сумме значений числа узлов в базовой сетке и удвоенного
числа узлов дополнительной сетки. Очевидно, что матрица
. Размерность
этой матрицы равна сумме значений числа узлов в базовой сетке и удвоенного
числа узлов дополнительной сетки. Очевидно, что матрица  ,
в результате предложенной аппроксимации, является слабо заполненной,
несимметричной, однако имеет симметричный портрет. Поэтому для хранения этой
разреженной матрицы используется разреженный строчный формат [9], что позволяет
существенным образом сократить затраты на память. Для решения системы линейных
алгебраических уравнений (СЛАУ) используется итерационный метод
стабилизированных бисопряженных градиентов BiCGStab [9].
,
в результате предложенной аппроксимации, является слабо заполненной,
несимметричной, однако имеет симметричный портрет. Поэтому для хранения этой
разреженной матрицы используется разреженный строчный формат [9], что позволяет
существенным образом сократить затраты на память. Для решения системы линейных
алгебраических уравнений (СЛАУ) используется итерационный метод
стабилизированных бисопряженных градиентов BiCGStab [9].
 с ровным дном
с ровным дном  ,
цилиндрический остров радиуса
,
цилиндрический остров радиуса  расположен в начале
координат. На горизонтальных границах расчетной области и на границе
острова заданы отражающие граничные условия, на вертикальных границах-заданы
открытые граничные условия.
расположен в начале
координат. На горизонтальных границах расчетной области и на границе
острова заданы отражающие граничные условия, на вертикальных границах-заданы
открытые граничные условия.
 волна с амплитудой
волна с амплитудой
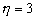 и длиной 10 расположена на позиции
и длиной 10 расположена на позиции  .
После этого она распадается на две уединенных волны, двигающихся в
противоположных направлениях.
.
После этого она распадается на две уединенных волны, двигающихся в
противоположных направлениях.














