Математическое моделирование распространения нелинейных волн на границе раздела неглубокого двухслойного потока вязкой жидкости
Архипов Дмитрий Григорьевич
Новосибирский государственный университет
1. Введение. Динамика потоков в стратифицированных средах в
последние годы вызывает большой интерес со стороны специалистов [1, 2].
Для волн в двухслойной системе существуют модели, в которых получаются
уравнения Кортевега – де Вриза. Одним из существенных недостатков этих
уравнений является то, что они не учитывают вязкости, и как следствие
диссипативных потерь, приводящих к уменьшению амплитуды волн по мере их
распространения. В работе [3] было
выведено эволюционное уравнение для внутренних волн в двухслойной системе с
учетом вязкости в отсутствие установившегося течения. Полученные результаты
численных расчетов по этому уравнению лучше описывают экспериментальные данные
[4–6], чем другие модели. С другой стороны, в статьях [7, 8] были
предложены уравнения, учитывающие стационарный поток, но в отсутствие вязкости.
Это исследование было ограничено лишь течениями с кусочно-постоянной зависимостью
скорости жидкости от глубины.
В данной работе
рассматривается стационарный поток в двухслойной системе между крышкой и дном.
Жидкость считается вязкой и в ней устанавливается вертикальный профиль
скорости. Устойчивость такого движения была показана в экспериментах [9] для случая
воды и минерального масла. В этом исследовании было обнаружено, что течение оказывается
устойчивым вплоть до скоростей, при которых в менее вязкой жидкости начинается
переход к турбулентности. Это позволяет рассматривать достаточно большой интервал
скоростей потока.
В отличие от статьи [3] при
выводе эволюционного уравнения существенную роль играет вид зависимости
вертикальной скорости от поперечной координаты. Поэтому было проведено
тщательное исследование влияния скорости потока на профиль вертикальной
скорости по глубине. В отсутствие стационарного течения эта зависимость
является практически линейной. При наличии неравномерного по глубине потока
такие исследования для одного слоя жидкости были проведены в работe [10].
Однако в ней пренебрегалось диссипацией, что приводило к особенности при
скоростях течения выше фазовой скорости распространения волны. В данной работе
показано, что для профиля вертикальной скорости вязкость имеет принципиальное
значение, и ею нельзя пренебрегать.
2. Постановка задачи. В плоском канале, ограниченном горизонтальными жесткими крышкой и дном, находятся два слоя жидкости различных по плотности, вязкости и глубине. Жидкость с меньшей плотностью располагается над более тяжелой жидкостью (стратификация устойчивая). Предполагается, что жидкости являются несжимаемыми и не перемешиваются. Обе жидкости двигаются под действием стационарного продольного градиента давления. В такой системе поперечная компонента скорости отсутствует, а вертикальный профиль горизонтальной скорости, состоит из участков парабол, т. е. имеет место двухслойное ламинарное течение Пуазейля (см, рис. 1):
, 
, 
,
, 
, 
,
где 
– скорость на границе раздела, 
,
- вязкости, 
,
- толщины жидкостей соответственно. Обозначим для определенности
характеристики верхней жидкости индексом 1, а нижней – 2. Таким образом, видно,
что профиль горизонтальной скорости зависит только от отношений вязкостей 
, и глубин 
жидкостей.
Рис. 1. Схема стационарных течения и трения, а также волнового процесса.
Наложим
возмущение на границу раздела жидкостей, используя ряд предположений
1)
амплитуда
возмущений существенно меньше глубины каждой из жидкостей 
~
(
– малый параметр);
2)
возмущения
являются длинноволновыми, т. е. характерный продольный размер волны заметно
больше глубин жидкостей 
~
;
3)
толщины вязких пограничных слоев для возмущения у крышки, дна и границы раздела значительно меньше глубин
жидкостей 
~
.
Кроме
того, будем рассматривать только такие скорости потока, при которых течение является
ламинарным. При этом система уравнений Навье-Стокса заметно упрощается и приводится
к следующему виду:
(1)
(2)
, (3)
Здесь t –
время, 
- возмущения горизонтальной и вертикальной составляющих скоростей
жидкостей, 
- кинематические вязкости, 
- плотности жидкостей, а 
- возмущения давлений
в слоях. Полная горизонтальная скорость, представляет сумму потоковой скорости
и скорости для возмущения: 
. 
Пренебрегая
поверхностным натяжением, поставим обычные краевые условия на границе раздела,
крышке и дне:
, 
, 
, при 
;
, 
при 
; 
, 
при 
;
где 
– возмущение границы
раздела, 
– трение жидкости, а
индексом i помечены значения величин на границе раздела.
В случае волн на поверхности однородной жидкости
аналогичная постановка задачи была
использована в статье [10].
3. Картина возмущенного течения. Для нахождения вертикального
профиля давления необходимо знать зависимости 
. Сначала рассмотрим задачу в первом приближении:
а) возмущения имеют бесконечно малую амплитуду; б) волны настолько длинны,
что давление обуславливается лишь гидростатикой, т. е. отсутствует дисперсия
возмущений; в) вязкий член пренебрежимо мал. В этих предположениях можно выбрать выражение для основных характеристик течения
в виде 
,
, 
(здесь i – мнимая единица, k – волновое число, 
– круговая частота).
В отсутствие потока получаем длинные линейные волны, бегущие
со скоростью 
. При наличии стационарного течения из уравнения (1),
используя уравнение неразрывности (3),
получаем линейное неоднородное обыкновенное дифференциальное уравнение
на профиль вертикальной скорости:
,
где 
– фазовая скорость
бесконечно длинных линейных волн.
Краевые условия в первом приближении имеют следующий простой
вид: на границе раздела 
, а на крышке и дне 
. Необходимо отметить, что четыре граничных условия для двух
уравнений первого порядка нужны для нахождения двух констант интегрирования и
собственных значений величин c и 
. Таким образом, мы имеем четыре условия и столько же
неизвестных. Это уравнение было решено и профиль вертикальной скорости
определяется следующим соотношением:
(4)
,
, 
.
Здесь 
- нормированная на 
вертикальная
скорость, коэффициенты 
, 
, 
– коэффициенты при степенях z в профиле потока каждого из слоев. Значения c и 
были найдены из
условий непротекания жидкостей на
крышке и дне. Графики 
при различных
скоростях потока представлены на рис. 2a. Видно, что при данных
параметрах профиль с увеличением скорости потока начинает становиться все более
нелинейным. Из решения (4) следует, что при условии 
функция 
оказывается равной
нулю на критическом уровне 
. Таким образом, возмущения не проникают в область за критический
уровень.
Рис. 2. Зависимости безразмерной поперечной
составляющей скорости (
) от безразмерной
вертикальной координаты z/H, при 
, 
мм, 
мм, 
мм2/с,
мм2/с
и различных значениях скорости стационарного потока (
); слева – рассчитанные по формуле (4), а справа –
вычисленные с учетом диссипации (
Гц).
При дальнейшем увеличении
скорости потока в рамках данного подхода анализ становится невозможным, так как
неоднородное решение уравнения стремится
к бесконечности при 
. Поэтому при отличной
от нуля правой части уравнения, решение
теряет смысл. В случае же, когда правая часть равна нулю, граничные условия
оказываются несовместными. С точки зрения математики это означает, что в такой
системе пренебрегать членом со старшей производной (диссипативный член)
недопустимо, хотя в отсутствие потока влияние вязкости сказывается лишь в
тонких пограничных слоях (см. рис. 2b).
Если
принять во внимание диссипацию возмущенного движения, то вид решения существенно
меняется, что и показано на графике (рис. 2b). Уравнение на профиль вертикальной
скорости с учетом вязкости имеет следующую форму:
.
В отличие от случая
идеальной жидкости неизвестные 
, c и 
теперь являются комплексными
величинами. Существенно изменяются, конечно же, и краевые условия на границе
раздела, крышке и дне:
, 
, 
, при z =
;
, 
при 
; 
,
при 
.
К сожалению, аналитического решения для этой задачи найдено не было. Поэтому был разработан численный алгоритм, который позволяет достаточно быстро находить решения с такими граничными условиями.
При решении этого уравнения «методом стрельбы» с дна и крышки параметров,
которые необходимо перебирать,
оказывается восемь: это комплексные 
, 
, c
и 
, т. е. их действительные и мнимые части. Перебирать по
такому количеству параметров, до тех пор, пока все граничные условия не будут выполнены,
было бы весьма затруднительным, но благодаря линейности системы перебор можно
существенно облегчить. Метод, использованный в программе, состоит в том, что
уравнение разделяется на однородное с граничными условиями на крышке и дне:
, 
, 
,
и неоднородное с граничными
условиями на крышке и дне:
, 
, 
.
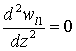Затем складываем эти решения
с коэффициентами 
и 
, необходимыми для удовлетворения граничным условиям: 
. Таким образом, вместо восьми параметров остается лишь два –
действительная и мнимая части фазовой скорости c. Последние краевые условия
на границе раздела 
, 
, где индексы R и I –
обозначают действительную и мнимую части, соответственно, выполняются путем перебора
по 
и 
. Вместо того, чтобы отслеживать выполнение двух граничных
условий, проверяется выполнение одного составного:
.
Таким образом, с на каждом следующем
шаге выбирается так, чтобы уменьшить левую часть данного равенства. Благодаря
этому существенно ускоряется поиск собственного значения.
Кроме того, были проведены
вычисления с учетом дисперсии возмущений для
kH, меняющегося в промежутке от 0 до 2. Однако существенного изменения профиля скорости,
как и предполагалось, не происходит. Учет нелинейных членов также вряд ли
приведет к заметным отклонениям. Поэтому для дальнейших расчетов будем
использовать приближение линейных профилей:
.
4.
Фазовая скорость и градиент давления на границе раздела. Проинтегрировав по координате
z уравнение движения (2) при l=2, получим:
.
Зависимость для давления в
верхнем слое находится аналогично. Теперь проинтегрируем уравнения (1) и
(3) по глубинам обоих слоев. Для начала
не будем рассматривать члены второго порядка малости, к ним мы вернемся ниже.
Продифференцировав первые из этих уравнений по координате x, а
вторые по времени, получим следующую систему уравнений:
, (5)
(6)
Давление на границе раздела исключается
путем умножения уравнения (5) на 
, а уравнения (6) на 
и последующего их
сложения. Таким способом, получаем эволюционное уравнение для очень длинных линейных
возмущений при наличии
установившегося течения:
, (7)
где введены обозначения:
, 
, 
, 
.
Будем искать решение
уравнения (11) в виде бегущей волны: 
.В итоге, получим простое квадратное уравнение на с:
.
Здесь использована формула 
. Решения этого уравнения можно записать в виде: 
. Из этого равенства видно, что в отсутствие потока, как и следовало
ожидать, получаем 
.
Найдем также градиент
давления на границе раздела, который понадобится ниже. Вычитая уравнение (6) из
уравнения (5), получим
. (8)
Таким образом, мы полностью
рассчитали задачу для случая длинных линейных волн при отсутствии диссипативных
потерь.
5. Течение в вязких пограничных слоях около всех границ.
Рассмотрим сперва линеаризованные уравнения (1) в окрестности уровня 
. Кроме того, будем считать, что в исследуемых нестационарных пограничных слоях практически не меняются скорость потока 
и ее производные вблизи границы раздела: 
= const. Тогда
(9).
Здесь мы воспользовались
тем, что для линейных волн, бегущих в направлении роста координаты x со
скоростью с, справедливо равенство: 
. Сделаем преобразование Лапласа по времени и получим
уравнение на функцию 
, являющуюся образом 
:
,
где 
– образ правой
(неоднородной) части уравнения (9), а 
– возмущенные скорости
жидкости в начальный момент времени, не зависящие от вертикальной координаты.
Это позволяет перенести член, содержащий 
в правую часть:
. В результате, получаем линейные дифференциальные уравнения
второго порядка:
.
Полагая пограничные слои
тонкими, перенесем граничные условия 
= 0 на 
(для верхней жидкости)
и на 
(для нижней).
Тогда искомые решения будут иметь
следующий вид:
,
Поставив теперь
условия сшивки на
границе раздела
, 
,
находим константы
и получаем
образ скорости на
границе раздела
и образ касательного напряжения
на границе раздела
Для нахождения этих величин
в зависимости от времени сделаем обратное преобразование Лапласа и подставим
формулу (8) для возмущения градиента
давления на границе
раздела. Тогда имеем
следующие формулы:
,
.
Проведем аналогичную
процедуру в пограничных слоях у крышки и дна, где скорость потока близка к нулю.
Полагая пограничные слои тонкими, перенесем граничные условия 
= 0 на 
(для нижней жидкости) и на 
(для верхней). Кроме
того, используем условия прилипания. В итоге получаем следующие формулы для трений о дно и крышку:
,
.
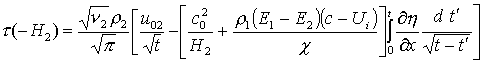6. Вывод эволюционного уравнения. Применим процедуру, которая
была использована для получения эволюционного уравнения в первом приближении,
но в этот раз проинтегрируем также нелинейные и диссипативные члены уравнения
(1) и будем сохранять величины второго
порядка малости. При этом воспользуемся соотношением из линейной
теории:
,
которое получается путем
непосредственного интегрирования уравнения неразрывности и подстановки граничных
условий на поверхности раздела. Использовать эту формулу можно при условии, что
волны двигаются в одном направлении, т. е. мы не рассматриваем встречного
взаимодействия нелинейных возмущений. Исключим градиент давления на
границе раздела в линейных
членах также, как
это было сделано
выше:
(10)
где введены обозначения
, 
.
Трения на всех границах и
скорость на поверхности раздела были определены выше. Градиент давления на
границе раздела был найден в первом приближении, и может быть использован в
нелинейном члене 
. Таким образом, все члены уравнения могут быть выражены
через возмущение границы раздела. В формуле, определяющей скорость жидкости на
поверхности раздела слоев
сделаем простую замену
,
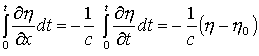и подставим начальные скорости, через начальное
возмущение границы:
.
Итак, мы получаем нелинейное
интегро-дифференциальное эволюционное уравнение для возмущения границы
раздела жидкостей:
(11)
Здесь введены
следующие обозначения:
,
,
, 
.
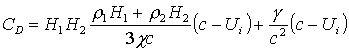
7. Решения эволюционного уравнения. Уравнение (11) можно
существенно упростить, если рассматривать трансформацию возмущений вне области
их возникновения. В этом случае, оба члена уравнения (11), которые содержат
начальное возмущение 
, окажутся равными нулю. Однако интегро-дифференциальное
уравнение, получающееся в итоге, все еще остается достаточно сложным для поиска
аналитических решений. Поэтому будем искать решения этого уравнения, считая
диссипацию возмущений малой, тем самым мы пренебрегаем интегральным членом и
получаем дифференциальное
уравнение:
, (12)
Такое
уравнение допускает решение в виде так называемых кноидальных волн, т.е.
периодических волн, не меняющих своей формы и бегущих с постоянной скоростью.
Обыкновенное дифференциальное уравнение для стационарно-бегущих волн получается
путем перехода в систему координат, двигающуюся со скоростью распространения
волны U (координата
). В этих переменных уравнение имеет следующий простой вид:
. (13)
Здесь 
– константа
интегрирования. Решения его хорошо известны (см, например [11, 12]) и
выражаются через эллиптические функции Якоби:
,
где
s – параметр, определяющий
меру нелинейности волны, L – длина кноидальной волны,
зависящая от амплитуды возмущения и параметра s:
,
а для скорости таких волн находим следующее соотношение:
.
В пределе,
когда параметр s стремится к единице, длина волны растет, и
получаем уединенное возмущение
типа солитона:
.
Скорость солитона
соответственно определяется равенством:
.
Графики кноидальных волн и уединенных возмущений при различных скоростях потока приведены на рис. 3. В зависимости от отношения глубин слоев мы можем получить волны с острыми пиками вверх или вниз. Нелинейность волн хорошо обнаруживается сравнением ширины горба и впадины (для линейных возмущений они были бы равными). Солитон в двухслойной системе также может быть ориентирован вверх или вниз. Видно, что при спутном потоке, т.е. когда скорости потока и волны совпадают по направлению, длина стационарных волн увеличивается, а при противотоке наоборот уменьшается.
Рис. 3. Формы
кноидальных волн при 
, 
, 
, 
, 
(слева), 
(справа) и
различных скоростях течения.
Для численного решения уравнения (11) на каждом шаге нужно вычислять интеграл, стоящий в правой части уравнения. Учитывая то, что этот интеграл не является аддитивным, то есть для следующего шага мы не можем пользоваться расчетом для предыдущего шага, объем вычислений очень велик и требует значительных затрат машинного времени. В случае, когда мы рассматриваем эволюцию вне области начального возмущения, справедливы соотношения
.
Последнее равенство связано с тем, что квадратный корень из отрицательного числа чисто мнимый. Это позволяет воспользоваться свойством Фурье-образа от свертки функций. Для анализа влияния трения на уединенную волну, интеграл был посчитан как прямым интегрированием, так и методом быстрого Фурье-преобразования. Скорость вычисления методом Фурье существенно превосходит скорость прямого вычисления интеграла при достаточном количестве точек, что показывает целесообразность его использования для численного решения эволюционного уравнения.
8. Заключение. Сформулируем основные результаты данной работы:
1)
Проанализировано
влияние потока на профиль вертикальной скорости для случаев идеальной и вязкой
жидкостей. Обнаружено, что диссипация оказывает существенное влияние на картину
течения при относительно высоких скоростях
потока.
2)
Выведено
эволюционное интегро-дифференциальное уравнение для возмущения границы раздела
установившегося потока двухслойной жидкости в горизонтальном канале, учитывающее
длинноволновые вклады инерции слоев, слабую нелинейность возмущений и
нестационарные трения на
всех границах системы.
3)
При
пренебрежении диссипативными потерями для возмущенного течения получены
стационарно-бегущие решения типа кноидальных волн и солитонов. Показано, что при спутном потоке длина установившихся
волн увеличивается, а при противотоке наоборот уменьшается.
Литература
1.
Степанянц Ю.А., Фабрикант А.Л. Распространение волн
в сдвиговых потоках. М.: Наука, 1996, 240 с.
2.
Ляпидевский В.Ю. и Тешуков В.М. Математические
модели распространения длинных волн в неоднородной жидкости. Новосибирск:
Изд-во СО РАН, 2000, 420 с.
3.
Хабахпашев Г.А. Эволюция возмущений границы раздела
двух слоев вязкой жидкости. Изв. АН СССР, Механика жидкости и газа, 1990,
№ 6, с. 118—123.
4.
Koop C.G., Butler G.
An investigation of internal solitary waves in a two-fluid system. J. Fluid
Mech., 1981, V. 112, P. 225 – 251.
5.
Segur H. Hammack J.
L. Solitary models of long internal waves. J. Fluid Mech., 1982, vol. 118, p.
285–304.
6.
Гаврилов Н. В. Вязкое затухание уединенных
внутренних волн в двухслойной жидкости. Прикл. мех. техн. физ., 1988, т. 29, №
4, с. 51–55.
7.
Пелиновский Е.Н., Полухина О.Е., Лэмб К. Нелинейные
внутренние волны в океане, стратифицированном по плотности и течению.
Океанология, 2000, т. 40, № 6, с. 805–815.
8.
Пелиновский Е.Н., Степанянц Ю.А., Талипова Т.Г.
Моделирование распространения нелинейных внутренних волн в горизонтально
неоднородном океане. Изв. РАН. Физика атмосферы и океана, 1994, т. 30, № 1, с.
79–85.
9.
Kao T.W., Park C.
Experimental investigation of the stability of channel flow. Part 2.
Two-layered co-current flow in a rectangular channel. J. Fluid Mech., 1972,
vol. 52, № 3, p. 401–423.
10.
Velthuizen H.G.M.,
van Wijngaarden L. Gravity waves over a non-uniform flow. J. Fluid Mech., 1969,
vol. 39, № 4, p. 817–829.
11.
Карпман В. И. Нелинейные волны в диспергирующих
средах. М.: Наука, 1973, 175 с.
12.
Уизем Дж. Линейные и нелинейные волны. М.: Мир,
1977, 622 с.