
В настоящее время в связи с проблемами геофизики, океанологии и физики атмосферы, а также в связи с использованием криогенных жидкостей в технике и рядом других проблем повышенный интерес вызывают задачи о распространении внутренних волн и колебаний в стратифицированных жидкостях. Под стратифицированной жидкостью принято понимать жидкость, физические характеристики которой (плотность, теплоемкость, динамическая вязкость и др.) в стационарном состоянии меняются непрерывно или скачком лишь в одном выделенном направлении. Наиболее существенное влияние, по сравнению с другими видами стратификации, оказывает стратификация плотности [1].
При численном решении моделей движения жидкости со стратификацией по плотности возникают системы линейных алгебраических уравнений с одинаковой на каждом слое по времени матрицей и различными правыми частями. Свойства матрицы этих систем таковы, что решение их с помощью методов расщепления [2-4] сопряжено с рядом трудностей, использование же итерационных методов на каждом временном слое требует знания свойств матрицы решаемой системы. Например, применение чебышевского метода затруднено, т.к. могут быть неизвестны минимальное и максимальное собственные числа матрицы или она может быть не самосопряженной. Использование же градиентных методов может быть не целесообразным из-за большого количества арифметических операций при их реализации. В связи с этим возникает необходимость в использовании методов, которые имеют скорость сходимости как у чебышевского итерационного метода и при этом используют минимальную информацию о свойствах матрицы решаемой СЛАУ.
1. Постановка задачи.
Будем рассматривать двумерные движения идеальной стратифицированной жидкости. В декартовой системе координат (x1,x3) такие движения описываются уравнением [1]
 |
(1) |
где функция u(x1,x3,t) такова, что
 (
( - функция тока);
- функция тока);
 - частота Вейсяля-Брента;
- частота Вейсяля-Брента; 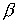 - некоторая положительная постоянная, задающая параметры стратификации жидкости;
g - ускорение свободного падения. К уравнению (1) необходимо добавить следующие начальные условия
- некоторая положительная постоянная, задающая параметры стратификации жидкости;
g - ускорение свободного падения. К уравнению (1) необходимо добавить следующие начальные условия
 . . |
(2) |
Исходное уранение решается в области
 |
(3) |
 , , |
(4) |
 . . |
(5) |
Рассматриваемая задача имеет две особенности. Во-первых, исходная дифференциальная задача задана на бесконечной области, и для единственности решения не требует задания краевого условия на бесконечности. Следовательно, при численном решении в ограниченной области краевого условия на "открытой" границе ставить нельзя. Во-вторых, при решении уравнения (1) разностными методами любая разностная схема, аппроксимирующая (1) будет пятидиагональная.
2. Аппроксимация.
Дифференциальное уранение (1) было аппроксимировано на неравномерной прямоугольной сетке узлов
 ,
,
 ,
,
 (
( ,
, 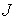 - множества индексов)
разностной схемой
- множества индексов)
разностной схемой
 , ,  , ,  , , |
(6) |

 , ,  . . |
(7) |
 - единичный оператор,
- единичный оператор,  ,
,  ,
,  ,
,  ,
,  ,
,  - шаг по времени.
- шаг по времени.
Таким образом для решения поставленной дискретной задачи необходимо решать на каждом n+1 слое по времени систему линейных алгебраических уравнений
 , , |
(8) |
 - неизвестный вектор (
- неизвестный вектор ( ,
,
 ),
f - известный вектор, зависящий то граничных условий и
решения на n и n-1 слоях по времени.
),
f - известный вектор, зависящий то граничных условий и
решения на n и n-1 слоях по времени.
В силу того, что область решения уравнения (1) не
ограничена, матрица и вектора системы (8) будут
содержать бесконечное число элементов. Поэтому при численном
решении необходимо ограничиваеть область  прямой
прямой
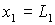 , на которой должно выполняеться само уравнение
(1). Вследствие чего, индекс i будет ограничен
постоянной m1 в точке
, на которой должно выполняеться само уравнение
(1). Вследствие чего, индекс i будет ограничен
постоянной m1 в точке
 .
.
В этом случае система (8) будет недоопределенной и
возникнет необходимость ее доопределения на прямой
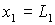 .
В силу того, что на ней должно быть выполнено само уравнение
(1), предлагается замыкать систему (8) путем
его аппроксимации внутрь области решения. Такая аппроксимация
имеет вид:
.
В силу того, что на ней должно быть выполнено само уравнение
(1), предлагается замыкать систему (8) путем
его аппроксимации внутрь области решения. Такая аппроксимация
имеет вид:
 , ,  , , , , . . |
(9) |
Для решения систем подобных полученной существует достаточно
богатый арсенал методов [2-4]. Например, пользуясь тем, что матрица системы (8) не
меняется при переходе от слоя к слою по времени, выгодно было бы
использовать чебышевский итерационный метод. Но для его реализации
требуется найти значения  и
и
 спектральных границ оператора A, что представляет собой отдельную,
достаточно трудоемкую задачу. Кроме того, при использовании их
приближенных значений, чебышевский итерационный метод является неустойчивым [2].
спектральных границ оператора A, что представляет собой отдельную,
достаточно трудоемкую задачу. Кроме того, при использовании их
приближенных значений, чебышевский итерационный метод является неустойчивым [2].
Все вышеуказанное верно, если матрица системы самосопряжена, но в нашем случае это условие не выполнется. В связи с этим возникает необходимость в использовании метода, который имеет оценку сходимости чебышевского итерационного метода, является сходящимся при неточном задании использующихся входных параметров и может быть использован в случае несамосопряженной матрицы A. В качестве такого метода была использована многошаговая итерационная схема (см. [5,6]).
2. Метод решения.
Пусть D - самосопряженный положительно
определенный оператор, действующий в m-мерном гильбертовом
пространстве Hm. Введем энергетическое подпространство HD,
состоящее из элементов Hm со скалярным произведением  и нормой
и нормой  . Пусть уравнение
(8) задано в этом пространстве Hm. Рассмотрим итерационную схему [5,6]
. Пусть уравнение
(8) задано в этом пространстве Hm. Рассмотрим итерационную схему [5,6]
 , , |
(10) |
 , , , , , ,
 , ,
 , ,
 , , |
(11) |
где  - значение оптимального итерационного параметра одношаговой итерационной схемы;
S0 - оператор шага одношаговой итерационной схемы;
- значение оптимального итерационного параметра одношаговой итерационной схемы;
S0 - оператор шага одношаговой итерационной схемы;  - норма этого оператора при оптимальном значении итерационного параметра.
- норма этого оператора при оптимальном значении итерационного параметра.
Для данной итерационной схемы в HD справедлива оценка [5,6]

 .
Таким образом, если известны постоянные
.
Таким образом, если известны постоянные
 и
и
 , то схема (10-11) сходится как
чебышевский итерационный процесс.
, то схема (10-11) сходится как
чебышевский итерационный процесс.
Предположим, что вместо  нам известно некоторое его
приближение
нам известно некоторое его
приближение  , выбранное, например, экспериментально, и соответствующая ему величина нормы опреатора шага
, выбранное, например, экспериментально, и соответствующая ему величина нормы опреатора шага  . В этом случае точное значение
. В этом случае точное значение  обычно
неизвестно и вместо него используется некоторая оценка
обычно
неизвестно и вместо него используется некоторая оценка
 .
Тогда можно показать [5,6], что если справедливо неравенство
.
Тогда можно показать [5,6], что если справедливо неравенство
 , , |
(12) |
то для оператора Gk справедлива оценка
 ,
,  ,
,где

причем во втором случае  и метод сходится со скоростью чебышевского итерационного процесса в
соответствии со значением
и метод сходится со скоростью чебышевского итерационного процесса в
соответствии со значением  .
.
При расчетах была использована следующая реализация многошаговой итерационной схемы:
 , ,
 , , |
(13) |
где  ,
,  ,
,  .
.
Коэффициэнты  вычисляются по следующим рекурентным формулам
вычисляются по следующим рекурентным формулам
 , ,  , ,  |
(14) |
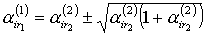 , ,  , ,  |
(15) |
где  ,
,
 ,
,
 .
Здесь
.
Здесь  может быть как точным, так и приближенным
значением оптимального параметра одношаговой итерационной схемы.
Причем, в качестве
может быть как точным, так и приближенным
значением оптимального параметра одношаговой итерационной схемы.
Причем, в качестве  можно использовать оценку
можно использовать оценку  .
.
Следует заметить, что самосопряженность оператора DB-1A используется только при оценке скорости сходимости алгоритма (13-15) и не требуется при его реализации. Это делает возможным применение многошаговой итерационной схемы и в случае несамосопряженного оператора A.
4. Модельные расчеты.
Для практической проверки свойств рассмотренного метода была проведена серия численных экспериментов на модельной задаче, в качестве которой была использована задача Дирихле для уравнение Пуассона заданного в единичном квадрате с границей Г.
 |
(16) |
 |
(17) |
Уравнение (16) аппроксимировалось на квадратной сетке
узлов с шагом  разностной схемой второго порядка
аппроксимации. Полученная система линейных уранений имеет
самосопряженную положительноопределенную матрицу, границы спектра
которой известны точно.
разностной схемой второго порядка
аппроксимации. Полученная система линейных уранений имеет
самосопряженную положительноопределенную матрицу, границы спектра
которой известны точно.
Решение этой системы проводилось явным 2p-циклическим чебышевским методом с упорядочиванием параметоров по Самарскому [2] и многошаговой схемой (13-15). Начальный вектор во всех расчетах брался единичным.
В таблице 1 приведены результаты расчетов при заданных
точно границах спектра  и
и  оператора A. При
этом
оператора A. При
этом  ,
,
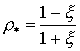 ,
,
 . Здесь p - величина,
определяющая длину цикла итерационных параметров; Nch -
количество итераций чебышевского метода; Nm - количество
итераций многошаговой схемы. Итерации останавливались при выполнения условия
. Здесь p - величина,
определяющая длину цикла итерационных параметров; Nch -
количество итераций чебышевского метода; Nm - количество
итераций многошаговой схемы. Итерации останавливались при выполнения условия  .
.
| M=50 | M=100 | M=150 | ||||
| Nch | Nm | Nch | Nm | Nch | Nm | |
| 2 | 884 | 723 | 3420 | 2867 | 7864 | 6671 |
| 3 | 528 | 415 | 1864 | 1279 | 4112 | 3127 |
| 4 | 304 | 206 | 1040 | 702 | 2160 | 1438 |
| 5 | 223 | 151 | 608 | 350 | 1184 | 670 |
| 6 | 176 | 134 | 447 | 253 | 768 | 382 |
В таблице 2 приведено число итераций получаемое при
решении модельной задачи схемой (13-15) при p=6 и M=50 для
различных значений  . Итерационный параметр
. Итерационный параметр  при этом задавался точно
при этом задавался точно  . Итерации останавливались при выполнения условия
. Итерации останавливались при выполнения условия  .
.
 .
. |
Nm |
| 0.001 | 2253 |
| 0.400 | 2065 |
| 0.990 | 308 |
 =0.998026 =0.998026 |
134 |
| 0.999 | 158 |
| 0.9999 | 446 |
| 0.99999 | 1791 |
| 0.999999 | 7167 |
В силу того, что построение и реализация многошаговой схемы
(10-11) не использует свойство
самосопряженности оператора A, мы посчитали целесообразным
проверить возможность использования этой схемы в несамосопряженном
случае. Для получения СЛАУ с несамосопряженным оператором в задаче
(16-17) на стороне квадрата x1=1 заменили
граничное условие  на
на
 и полученную дифференциальную задачу
аппроксимировали на квадратной сетке узлов разностной схемой
второго порядка аппроксимации внутри области и первого порядка при
x1=1. В итоге получили СЛАУ с несамосопряженным и
знакоопределенным оператором A. В таблице 3 приведены
результаты вычислений многошаговой схемой для M=25, M=150 и
различных значений
и полученную дифференциальную задачу
аппроксимировали на квадратной сетке узлов разностной схемой
второго порядка аппроксимации внутри области и первого порядка при
x1=1. В итоге получили СЛАУ с несамосопряженным и
знакоопределенным оператором A. В таблице 3 приведены
результаты вычислений многошаговой схемой для M=25, M=150 и
различных значений  выбранных экспериментально.Для определения значения параметра
выбранных экспериментально.Для определения значения параметра  ,
необходимого для построения метода, при выбранном
,
необходимого для построения метода, при выбранном  проводилось Nc итераций одношаговой схемой и
проводилось Nc итераций одношаговой схемой и  определялось с помощью выражения
определялось с помощью выражения  . Для
M=25 значение Nc=100, а для M=150 Nc=1000.
. Для
M=25 значение Nc=100, а для M=150 Nc=1000.
Заметим, что метод минимальных невязок сходится при тех же условиях для M=25 за 1535 итераций и за 44962 итерации при M=150.
| p | ||||||
 =0.0001 =0.0001 |
 =0.0003 =0.0003 |
 =0.0004 =0.0004 |
 =0.000005 =0.000005 |
 =0.00001 =0.00001 |
 =0.000011 =0.000011 |
|
| 2 | 1704 | 564 | 414 | 25216 | 12622 | 11478 |
| 3 | 1074 | 352 | 241 | 12962 | 6512 | 5928 |
| 4 | 896 | 288 | 176 | 7168 | 3648 | 3328 |
| 5 | 872 | 276 | 160 | 4832 | 2512 | 2304 |
5. Решение задачи о движении стратифицированной жидкости.
При решении задачи (1-5) функция  из (5) задавалась в виде
из (5) задавалась в виде
 |
(18) |
 |
(19) |
s - параметр, влияющий на скорость потока на границе x1=0 для времени t>6·10-3.
Функция (18) задана таким образом, что на входе в канал у вектора скорости отсутствует вертикальная составляющая.

 при s=0.
при s=0.

 при s=0.05.
при s=0.05.
На рисунках 1 и 2 показаны линии уровня
функции  для времени t=0.02 - вариант "a", t=0.5 -
вариант "b", "t=1" - вариант "c". Во всех расчетах
значение параметра стратификации
для времени t=0.02 - вариант "a", t=0.5 -
вариант "b", "t=1" - вариант "c". Во всех расчетах
значение параметра стратификации 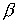 =5. При этом область
решения изображена на рисунках не полностью, а только та ее часть,
где наблюдается возмущение.
=5. При этом область
решения изображена на рисунках не полностью, а только та ее часть,
где наблюдается возмущение.
Рисунок 1 показывает решение полученное для s=0.
Такое значений s предполагает, что для времени t>6·10-3
жидкость не проходит через границу области x1=0. Для
рисунка 2 параметр s=0.05. В этом случае для любого
значения  через границу x1=0 поступает жидкость.
через границу x1=0 поступает жидкость.
Во время всех вычислений бралась область  ,
число узлов
,
число узлов  =301,
=301,
 =51. Шаг по времени
=51. Шаг по времени
 =10-3.
На первом этапе для найденных
экспериментально значений
=10-3.
На первом этапе для найденных
экспериментально значений  ,
,
 согласно
(14-15) строился набор итерационных параметров
в количестве 2p (p=15). Далее для каждого слоя
по времени с помощью многошаговой итерационной схемы решалась СЛАУ с
использованием полученных параметров.
Итерации продолжались до выполнения условия
согласно
(14-15) строился набор итерационных параметров
в количестве 2p (p=15). Далее для каждого слоя
по времени с помощью многошаговой итерационной схемы решалась СЛАУ с
использованием полученных параметров.
Итерации продолжались до выполнения условия
 . Среднее
количество итераций на каждом слое по времени составило 178.
. Среднее
количество итераций на каждом слое по времени составило 178.
Список литературы