Реконструкция изображений в оптической томографии с помощью метода Левенберга-Маркварта
Иванов Д.Н. Бондаренко А.Н.
Новосибирский государственный
технический университет
Оптическую томографию можно определить как задачу восстановления
пространственно изменяющихся карт оптических параметров, главным образом
коэффициенты поглощения и рассеяния, из дискретного множества измерений
переданного и/или отраженного излучения. Когда рассматриваются медицинские
приложения, которым уделяют наибольшее внимание, значимый частотный спектр
лежит в ближнем инфра-красном диапазоне, 700-1000 нм, в котором ткань является
относительно прозрачной.
Схема измерения для оптической томографии состоит из S источников, расположенных
в позициях  на
границе тела
на
границе тела  и
M детекторов, расположенных в позициях
и
M детекторов, расположенных в позициях
 приведено на рис.1
приведено на рис.1
Наиболее строгий подход к анализу распространения света в среде
заключается в решении уравнения переноса излучения вид которого
для монохроматического света имеет вид
Здесь  - лучевая
интенсивность света, рассеянного в момент времени t в точке r в направлении
- лучевая
интенсивность света, рассеянного в момент времени t в точке r в направлении
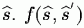 - фазовая функция,
определяющая часть лучевой интенсивности, которая рассеивается частицей
в направлении
- фазовая функция,
определяющая часть лучевой интенсивности, которая рассеивается частицей
в направлении  при условии,
что падающая на частицу волна направлена вдоль
при условии,
что падающая на частицу волна направлена вдоль
 - скорость частиц в среде,
- скорость частиц в среде,
 - полное
сечение, где
- полное
сечение, где  - сечение рассеяния
и
- сечение рассеяния
и  - сечение
поглощения. Функция
- сечение
поглощения. Функция  - функция источника.
Введем плотность числа частиц
а также поток частиц
Практический интерес представляет не сама функция
- функция источника.
Введем плотность числа частиц
а также поток частиц
Практический интерес представляет не сама функция  ,
а интегралы от нее по некоторым областям фазового пространства
,
а интегралы от нее по некоторым областям фазового пространства
 . При оптическом
зондировании биотканей измеряемой величиной является функция распределения
выходящего излечения на поверхности среды (светимость)
. При оптическом
зондировании биотканей измеряемой величиной является функция распределения
выходящего излечения на поверхности среды (светимость)  Интегро-дифференциальное уравнение (1) является сложным для анализа
распространения света в рассеивающих средах, поэтому оно упрощается
путем представления решения и функции источника в ряд по сферическим
гармоникам. Такое упрощение приводит к системе из
Интегро-дифференциальное уравнение (1) является сложным для анализа
распространения света в рассеивающих средах, поэтому оно упрощается
путем представления решения и функции источника в ряд по сферическим
гармоникам. Такое упрощение приводит к системе из  связанных дифференциальных уравнений в частных производных, известное как
связанных дифференциальных уравнений в частных производных, известное как
 приближение.
При N=1 получается четыре связанных дифференциальных уравнения, которые,
используя (2) и (3) сводятся к следующим уравнениям
В диффузионном приближении для уравнений (5)-(6) предпологается, что
приближение.
При N=1 получается четыре связанных дифференциальных уравнения, которые,
используя (2) и (3) сводятся к следующим уравнениям
В диффузионном приближении для уравнений (5)-(6) предпологается, что
 и
и
 .
Используя эти предположения, уравнение (6) упрощается в закон Фика
где
.
Используя эти предположения, уравнение (6) упрощается в закон Фика
где  - коэффициент
диффузии света в среде.
Подставляя (7) в (5) получим уравнение диффузии
Применяя преобразование Фурье к уравнению (8) получим уравнение
диффузии в частотном случае ("Frequency-domain")
Условие для
- коэффициент
диффузии света в среде.
Подставляя (7) в (5) получим уравнение диффузии
Применяя преобразование Фурье к уравнению (8) получим уравнение
диффузии в частотном случае ("Frequency-domain")
Условие для  на
границе
на
границе  рассеивающей и
нерассеивающей сред следует из условия равенства нулю потока энергии внутрь
среды
где
рассеивающей и
нерассеивающей сред следует из условия равенства нулю потока энергии внутрь
среды
где  .
Параметр R - эффективный коэффициент отражения.
.
Параметр R - эффективный коэффициент отражения.
Рассмотрим следующее уравнение
Уравнению (11) соответствует следующая система из двух уравнений
где  и
и
 соответственно
вещественная и мнимая части комплексной функции
соответственно
вещественная и мнимая части комплексной функции
 из уравнения (11).
Запишем для системы (12) эквивалентную вариационную формулировку
Представим функции
из уравнения (11).
Запишем для системы (12) эквивалентную вариационную формулировку
Представим функции  и
и  в виде линейной комбинации
базисных функций
Подставляя (14) и (15) в (13) получаем следующую СЛАУ для компонент
в виде линейной комбинации
базисных функций
Подставляя (14) и (15) в (13) получаем следующую СЛАУ для компонент
 .
Обозначим через
.
Обозначим через  и
и
 интегралы из
системы (16), то есть
Локальная матрица конечного элемента
интегралы из
системы (16), то есть
Локальная матрица конечного элемента
 выглядит
следующим образом:
Будем рассматриваем нашу задачу на треугольной сетке, то есть разбиваем
расчетную область на конечные элементы - треугольники. На каждом конечном
элементе
выглядит
следующим образом:
Будем рассматриваем нашу задачу на треугольной сетке, то есть разбиваем
расчетную область на конечные элементы - треугольники. На каждом конечном
элементе  треугольной сетки определим три локальных базисных функции
Представим параметры
треугольной сетки определим три локальных базисных функции
Представим параметры  и
и  на каждом
конечном элементе
на каждом
конечном элементе  в виде интерполянтов, то есть
где
в виде интерполянтов, то есть
где  - узлы конечного
элемента
- узлы конечного
элемента  ,
,
 - его локальные базисные функции.
Учитывая представление (17) функций
- его локальные базисные функции.
Учитывая представление (17) функций  на
на  , получим
выражения для интеграла
, получим
выражения для интеграла 
Большинство точных подходов для решения задачи оптической
томографии основываются на нелинейном LS подходе. LS целевой
функционал для решения задачи оптической томографии записывается в
виде
Коэффициенты  и
и  представлены в следующем виде
Функции
представлены в следующем виде
Функции  и
и
 типичные
локально-базисные функции, такие как узловые базисные функции
конечно-элементной сетки.
Внутри разложения (18)-(19) коэффициенты
типичные
локально-базисные функции, такие как узловые базисные функции
конечно-элементной сетки.
Внутри разложения (18)-(19) коэффициенты  отождествляем с векторами
и вектор параметров для обратной задачи представляем в виде
Итерационный шаг метода Левенберга-Маркварта вычисляется как
Якобиан записывается в виде
где
отождествляем с векторами
и вектор параметров для обратной задачи представляем в виде
Итерационный шаг метода Левенберга-Маркварта вычисляется как
Якобиан записывается в виде
где  есть прямое отбражение для k источника.
Для получения элементов матрицы J мы используем разложения
(18)-(19) для элементов матрицы $A$, которые
записываются в виде
где
Дифференцируя конечно-элементную аппроксимацию по соответствующим
коэффициентам
есть прямое отбражение для k источника.
Для получения элементов матрицы J мы используем разложения
(18)-(19) для элементов матрицы $A$, которые
записываются в виде
где
Дифференцируя конечно-элементную аппроксимацию по соответствующим
коэффициентам  получим
получим
Рис. 2: Данные для обратной задачи
|
|
Рис. 3: Результат восстановления с 1 источником
|
|
Рис. 4: Результат восстановления с 2 источниками
|
|
В результате
проделанной работы был разработан алгоритм и реализован программный комплекс,
позволяющий моделировать распространение света в среде в диффузионном
приближении. Данный программный комплекс также позволяет восстанавливать
коэффициенты рассеяния и поглощения по измереным данным.
![]() на
границе тела
на
границе тела ![]() и
M детекторов, расположенных в позициях
и
M детекторов, расположенных в позициях
![]() приведено на рис.1
приведено на рис.1





















