


| § 4. Метод Ньютона | 
|
... это они от радости усложняют, из увлечения умственным
— Ну,
А. Платонов. Чевенгур
Здесь описывается и обсуждается важнейший метод второго порядка - метод Ньютона.
4.1. Эвристические соображения, приводящие к методу Ньютона безусловной оптимизации.
Если исходить из того, что необходимым этапом нахождения решения задачи
| f(x) → min, | (1) |
где f: Rm → R, является этап нахождения стационарных точек,
| F(x) ≝ f ′(x) = Θ, | (2) |
(обозначение F для f ′ мы будем сохранять на протяжении всего параграфа), то можно попытаться решать уравнение (2) известным методом Ньютона решения нелинейных уравнений
| xn+1 = xn – [F ′(xn)]–1F(xn). | (3) |
Для задачи (1) этот метод называется методом Ньютона безусловной оптимизации и задается формулой
| xn+1 = xn – [f ′′(xn)]–1f ′(xn). | (4) |
Формула (3) может быть выведена, исходя из следующих соображений. Пусть
| F(x) ≈ Φ(x) ≝ F(xn) + F ′(xn)(x – xn) |
и взять в качестве следующего приближения решение уравнения
| Φ(x) = Θ, | (5) |
то мы получим формулу (3).
Применительно к задаче (1) эти соображения выглядят так. Пусть так же, как и в п. 3.2 у нас уже есть некоторое приближенное решение xn задачи (1). Заменим в ней функцию f ее приближением второго порядка:
|
и в качестве следующего приближения возьмем решение задачи
| φ(x) → min. | (6) |
З а д а ч а 4.1*. Докажите, что если f ′′(xn) > 0, то решение задачи (6) задается формулой (4).
Геометрическая интерпретация формул (3) и (4) приведена на рис. 10а и 10б.
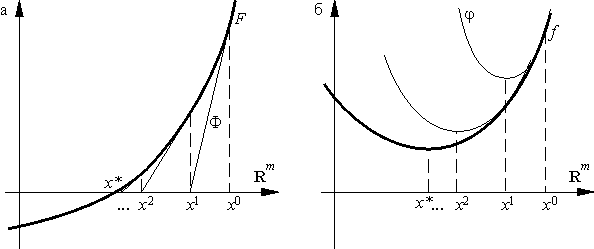
Метод Ньютона относится к методам второго порядка, поскольку для вычисления каждой итерации требуется знание второй производной функции f. По тем же соображениям градиентный метод относят к методам первого порядка. Подчеркнем, что здесь речь идет не о порядке сходимости метода, а о порядке используемых методом производных минимизируемой функции.
4.2. Теорема о локальной сверхлинейной сходимости метода Ньютона.
Пусть f дважды непрерывно дифференцируема,
Д о к а з а т е л ь с т в о. Очевидно,
| (7) |
Поскольку F ′(x*) невырожден, в силу (7) при x достаточно близких к x* невырожден
и оператор
|
Поэтому, в частности, при x достаточно близких к x*
| ||[F ′(x)]–1|| ≤ C. | (8) |
Далее, в силу того, что F дифференцируема, а
| F(x) = F(x*) + F ′(x*)(x – x*) + o(x – x*) = F ′(x*)(x – x*) + o(x – x*), |
Но тогда в силу (8)
|
x – x* – [F ′(x)]–1F(x) = [F ′(x)]–1F ′(x)(x – x*) – [F ′(x)]–1F(x) = = [F ′(x)]–1[F ′(x)(x – x*) – F(x)] = o(x – x*). |
или
| x – [F ′(x)]–1F(x) – x* = o(x – x*). |
|
xn+1 – x* = xn – [F ′(xn)]–1F(xn) – x* ≝ ≝ φ(xn – x*) = o(xn – x*). | (9) |
Возьмем теперь в качестве
|
и, следовательно, xn → x* при n→ ∞. Более того, для произвольного
4.3. Обсуждение метода Ньютона.
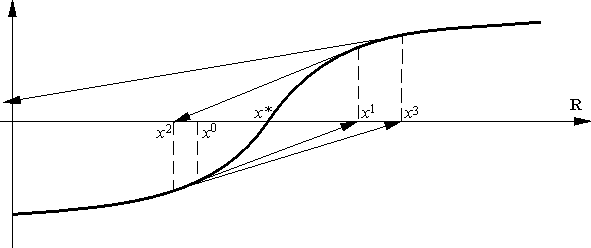
Таким образом, метод Ньютона, с одной стороны, может сходиться с более высоким чем градиентный метод порядком, а, с другой стороны, для его сходимости требуются достаточно хорошие начальные приближения (по крайней мере так требуется в доказанной теореме). Простой геометрический пример (см. рис. 11) подтверждает эту особенность метода (мы приводим пример для уравнения (2); соответствующий пример для задачи (1) получается "интегрированием" рис. 11).
Разумеется, как метод второго порядка, метод Ньютона требует большего объема вычислительной работы, поскольку приходится вычислять вторые производные функции f.
К этому сводятся основные преимущества (высокий порядок сходимости) и недостатки (локальный характер сходимости и больший объем вычислений) метода Ньютона.
Если функция f дополнительно сильно выпукла, то можно утверждать сходимость именно к решению задачи (1), а не только к стационарной точке функции f, и, кроме того, оценить радиус окрестности, из которой приближения Ньютона сходятся.
4.4. Теорема о квадратичной сходимости метода Ньютона.
Пусть
|
Тогда для
|
где q = L||f ′(x0)||/2λ2 < 1.
Д о к а з а т е л ь с т в о. По теореме 2.9
и 2.10 в условиях нашей теоремы решение x*
задачи (1) существует и единственно. Воспользуемся аналогом формулы
|
|
Вычитая из обеих частей этого равенства |
|
|
Положим в полученной оценке
||f ′(xn + h) – f ′(xn) + f ′′(xn)[f ′′(xn)]–1f ′(xn)|| = || f ′(xn+1)|| ≤
| (10) |
З а д а ч а 4.2*. Докажите, что если обратимый линейный оператор A на Rm
удовлетворяет оценке
Поскольку f сильно выпукла, в силу задачи 2.15, f ′′(xn) ≥ λ и поэтому (см. пред. задачу)
| (11) |
С помощью (11) индукцией по n легко доказывается неравенство
| (12) |
Наконец, в силу сильной выпуклости f, так как
| 0 ≥ f(x*) – f(xn) ≥ (f ′(xn), x* – xn) + λ||xn – x*|| 2, |
или
| (f ′(xn), xn – x*) ≥ λ|| xn – x*|| 2. |
Но тогда
|
λ||xn – x*|| 2 ≤ (f ′(x*), xn – x*) ≤ ||f ′(x*) |
откуда
4.5. Продолжение обсуждения метода Ньютона.
Из доказанной теоремы следует, что чем меньше константа Липшица отображения
З а д а ч а 4.3. Докажите.
Если снизить требования гладкости на функцию f, например, отказаться от условия Липшица для
З а д а ч а 4.4. Покажите, что для функции
Как позволяет думать теорема 4.4, метод Ньютона даже для сильно выпуклых функций в общем случае сходится лишь локально. В следующем пункте мы описываем модификации этого метода, которые могут обладать свойством глобальной сходимости.
4.6. Методы Ньютона с регулировкой шага.
Эти методы еще называют методами
| xn+1 = xn – αn[f ′′(xn)]–1f ′(xn). |
Длина шага может выбираться с помощью алгоритма дробления шага (см. п. 3.9), требуя, например, выполнения неравенства
|
f(xn+1) = f(xn –αn[f ′′(xn)]–1f ′(xn)) ≤ ≤ f(xn) – εαn(f ′(xn), [f ′′(xn)]–1f ′(xn)), |
| αn = argminα≥0{f(xn – α[f ′′(xn)]–1f ′(xn))}. |
Можно показать, что методы
4.7. Метод
Этот метод основан на следующей идее. Чтобы избежать расходимости приближений метода Ньютона, вызванных неудачным выбором начального приближения (см. рис. 11), можно попытаться запретить следующей итерации быть слишком далеко от предыдущей. Для этого следующую итерацию ищут из условия
| xn+1 = argmin φ(x) ≝ argmin {f(xn) + (f ′(xn), x – xn) + |
|
где ln — некоторый параметр (вообще говоря, свой на
каждом шаге). Первые три слагаемых в определении функции φ представляют собой квадратичную аппроксимацию функции f, а последнее
| Θ = φ′(x) = f ′(xn) + f ′′(xn)(x –xn) + ln(x– xn). |
Как легко видеть,
| xn+1 = argmin φ(x) = xn – [f ′′(xn) + lnI]–1f ′(xn). | (13) |
Последняя формула и есть метод
Очевидно, что если
|
| f(xn+1) ≤ f(xn) – ε2(yn, f ′(xn)), |
где ε1 ∈ (0, 1) и ε2 ∈ (0, 1/2) — параметры.
4.8. Еще один недостаток метода Ньютона. Модифицированный метод Ньютона.
В некоторых задачах более существенным недостатком метода Ньютона является его большая вычислительная трудность: на каждом шаге требуется вычисление оператора (матрицы)
| xn+1 = xn – [f ′′(x0)]–1f ′(xn). | (14) |
Геометрическая интерпретация модифицированного метода Ньютона (14) изображена на рис. 12.
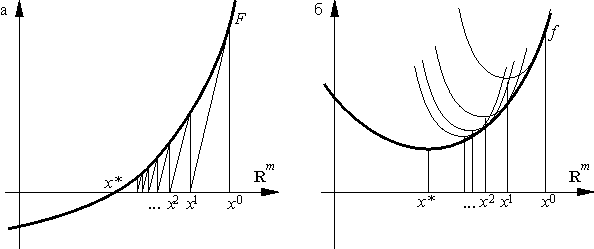
Можно показать, что при естественных ограничениях модифицированный метод Ньютона сходится лишь линейно (это плата за уменьшение объема вычислений). Можно также не замораживать оператор
| xn+1 = xn – [f ′′(x[n/k]·k)]–1f ′(xn); | (15) |
здесь [a] в верхнем индексе обозначает целую часть числа a. Можно
доказать, что если функция f сильно выпукла и
| ||xn+k – x*|| ≤ C||xn – x*||k+1, |
| ||xn+1 – x*|| ≤ C||xn – x*||k√k+1. |
Другими словами, метод (15) является методом
Другой способ уменьшения объема работы, связанного с вычислением функции
Напомним, что метод секущих решения уравнения (2) заключается в приближенной замене функции F в этом уравнении не касательной
|
который и называется методом секущих. Известно, что для достаточно гладких выпуклых функций порядок сходимости этого метода равен τ, где
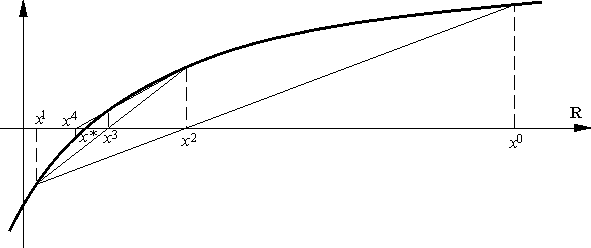
В многомерном случае поступают следующим образом. Пусть
|
(в общем положении эта точка единственна).
Несложные рассуждения показывают, что
| (16) |
Тогда
|
Затем описанные действия повторяются для точек
Отметим, что поскольку на каждом шаге в системе (16) меняется лишь один столбец, то ее решение на каждом шаге можно обновлять с помощью специальной процедуры, не требующей большого объема вычислений.
Отметим, что метод секущих, в отличие от ранее рассматривавшихся методов, не является одношаговым в том смысле, что для вычисления следующей итерации ему не достаточно информации, полученной на предыдущем
File based on translation from
TEX by TTH,
version 3.05.
Created 7 Jun 2002, 21: 38.