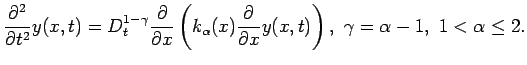 |
(1.1) |
УРАВНЕНИЙ ДРОБНОГО ПОРЯДКА НА КЛАСТЕРНЫХ СИСТЕМАХ
Лукащук С.Ю., Костригин И.В.
Уфимский государственный авиационный технический университет
В последние 10 лет наблюдается повышенный интерес к исследованию диффузионных процессов, не подчиняющихся закону Фика и не описываемых классическим уравнением диффузии [1,2]. Такие процессы наблюдаются на практике, в частности, в высокоэнергетической плазме, при переносе во фрактальных средах и в аморфных полупроводниках. Оказалось, что для математического описания таких процессов удобно использовать аппарат дробного интегродифференцирования. Однако, наличие в уравнении дробных производных приводит к существенным трудностям при построении как аналитических, так и численных решений. В связи с этим является актуальной задача разработки эффективных алгоритмов численного решения краевых задач для дифференциальных уравнений в частных производных дробного порядка.
Численное решение уравнений дробного порядка сопряжено с большими вычислительными трудностями, связанными, в первую очередь, с нарастанием объемов вычислений по мере увеличения значения временной переменной. Это обусловлено самой природой таких уравнений, которые учитывают так называемые эффекты памяти. В результате время расчета даже одномерной задачи на относительно грубой сетке может составлять несколько часов. Поэтому представляется оправданным привлечение для исследования уравнений с дробными производными многопроцессорной вычислительной техники, что влечет за собой необходимость соответствующей адаптации существующих методов и алгоритмов.
В данной работе рассматриваются некоторые подходы к численному решению одного класса дифференциальных уравнений дробного порядка, называемых диффузионно-волновыми.
![$\displaystyle D^{\alpha}f(t)=\frac{d^m}{dt^m}
\left[
\frac{1}{\Gamma(m-\alpha)}\int\limits_0^t\frac{f(\tau)}{(t-\tau)^{\alpha+1-m}}d\tau
\right],$](img5.gif) |
Разобьем область
![]() на
на ![]() отрезков с узлами
отрезков с узлами
![]() , где
, где
![]() . Временной интервал
. Временной интервал
![]() разобьем на части с шагом
разобьем на части с шагом ![]() и временными узлами
и временными узлами
![]() .
Для аппроксимации вторых производных по пространственной и временной переменным используем центральную разность, имеющую второй порядок точности:
.
Для аппроксимации вторых производных по пространственной и временной переменным используем центральную разность, имеющую второй порядок точности:
Для аппроксимации дробной производной Римана-Лиувилля воспользуемся формулой Грюнвалда [9] и L1-аппроксимацией [7]. В результате в первом случае получаем метод конечных разностей (МКР) для дробных производных, а во-втором случае приходим к L1-схеме.
Если ![]() непрерывна, а
непрерывна, а ![]() интегрируема на отрезке
интегрируема на отрезке ![]() , тогда для любого порядка
, тогда для любого порядка
![]() производные Римана - Лиувилля и Грюнвалда - Летникова существуют и совпадают для любого момента времени из
производные Римана - Лиувилля и Грюнвалда - Летникова существуют и совпадают для любого момента времени из ![]() [2].
[2].
Определение Грюнвалда - Летникова позволяет численно находить производную Римана - Лиувилля:
Порядок аппроксимации зависит от выбора коэффициентов
![]() . Аппроксимация будет иметь первый порядок точности, если
. Аппроксимация будет иметь первый порядок точности, если
![]() -
- ![]() -ый коэффициент в разложении
-ый коэффициент в разложении
![]() , т.е.
, т.е.
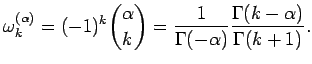 |
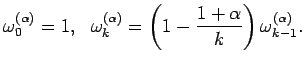 |
Важно отметить, что аппроксимация (1.6) справедлива, либо при
![]() , либо когда
, либо когда ![]() достаточна гладкая в окрестности
достаточна гладкая в окрестности ![]() [8].
[8].
Для простоты рассмотрим случай
![]() const
const![]() .
Уравнение (1.1), согласно (1.4) и (1.6), заменяется явным конечно-разностным уравнением
.
Уравнение (1.1), согласно (1.4) и (1.6), заменяется явным конечно-разностным уравнением ![]() :
:
Утверждение 1. Для устойчивости схемы (1.8) достаточно выполнения неравенства
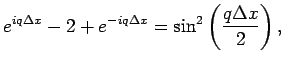
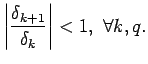
Положим
Если
![]() для некоторого
для некоторого ![]() , то схема неустойчива.
Из (1.11) следует, что если
, то схема неустойчива.
Из (1.11) следует, что если
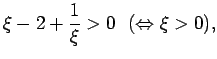
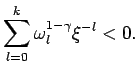
Заметим, что при ![]() имеем
имеем
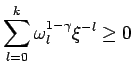
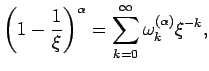 |
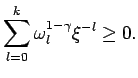
Теперь, если ![]() , то из (1.11) необходимо
, то из (1.11) необходимо
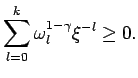
Используя подход, предложенный в [9], рассмотрим экстремальное значение ![]() . В результате получим условие устойчивости:
. В результате получим условие устойчивости:
Обозначим
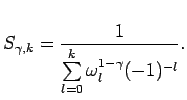
В [9] показано, что
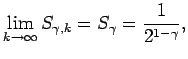
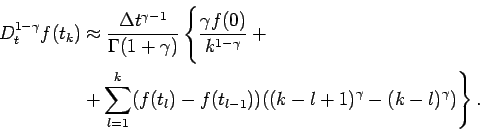 |
(1.13) |
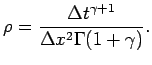
Положим
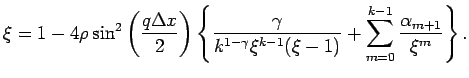 |
Знаменатель в (1.20) убывает для четных ![]() и возрастает для нечетных.
Поэтому можно записать:
и возрастает для нечетных.
Поэтому можно записать:
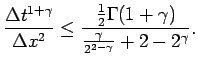 |
З а м е ч а н и е. Заметим, что как в выражении (1.9), так и в (1.16), при
![]() получим
получим
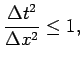 |
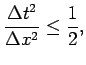 |
На каждом временном шаге происходит обмен между двумя соседними процессорами значениями искомой функции в крайних точках отрезках (2 числа типа double) (см. рисунок 2).
Отметим особенности разработанного параллельного алгоритма:
В силу указанных особенностей предлагаемые параллельные алгоритмы должные обладать достаточно высокой эффективностью, причем она будет тем выше, чем больше количество временных слоев. С целью проверки данного утверждения в работе выполнен ряд тестовых расчетов.
Проведем исследование эффективности параллельной реализации схем МКР и L1 на ряде тестовых задач.
Рассмотрим случай, когда коэффициент диффузии не зависит от координаты. Не ограничивая общности, можно положить его равным единице
![]() Начальные и граничные условия поставим следующим образом:
Начальные и граничные условия поставим следующим образом:
Отметим, что краевая задача (1.1), (2.1) аналогична задаче колебаний струны с закрепленными концами и допускает аналитическое решение вида:
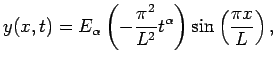 |
(2.2) |
где
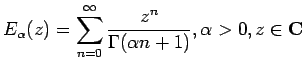 |
Результаты численного решения задачи при
![]() для различных моментов времени показаны на рисунке 3. На рисунке 4 показана временная эволюция центральной точки
для различных моментов времени показаны на рисунке 3. На рисунке 4 показана временная эволюция центральной точки ![]() . Хорошо видно затухание колебаний с течением времени. В этом проявляется существенное отличие диффузионно-волнового уравнения от обычного волнового. В первом случае затухание колебаний оказывается обусловлено структурой среды (напомним, что поскольку коэффициент диффузии постоянный, то среда изотропна). Для классического же волнового уравнения затухание может быть вызвано либо действием внешних сил (источниковых членов), либо неоднородностью среды.
. Хорошо видно затухание колебаний с течением времени. В этом проявляется существенное отличие диффузионно-волнового уравнения от обычного волнового. В первом случае затухание колебаний оказывается обусловлено структурой среды (напомним, что поскольку коэффициент диффузии постоянный, то среда изотропна). Для классического же волнового уравнения затухание может быть вызвано либо действием внешних сил (источниковых членов), либо неоднородностью среды.
На рисунке 5 показано изменение абсолютной погрешности численного решения задачи по схеме L1 для трех моментов времени. Из рисунка видно, что с увеличением времени погрешность убывает. Это объясняется свойствами как самого уравнения ("обладающего памятью"), так и свойствами разностной схемы.
В таблице 2 приведены значения времени решения задачи по схемам МКР и L1, при двух различных значениях шагов по пространственной переменной. Отметим, что уменьшение шага в два раза приводит к весьма существенному (более чем в 20 раз) увеличению времени счета. Это связано с резким увеличением количества суммируемых членов ряда, что, в свою очередь, следует из полученных в разделе 2 условий устойчивости.
|
|
На рисунках 6 и 7 показаны зависимости ускорения и эффективности параллельных алгоритмов от числа процессоров, полученные при тестовых расчетах на кластерной системе УГАТУ. Видно, что схема L1 показывает более высокие значения ускорения по сравнению с МКР. Более того, в L1 наблюдается почти линейная зависимость ускорения от числа процессоров, слабо зависящая от шага по пространству. Эффективность схемы L1 также оказывается выше. По результатам тестирования можно сделать вывод, что использование процедуры распараллеливания для численных схем решения задач с дробными производными оказывается весьма эффективным.
На рисунке 8 приведен график численного решения задачи (1.1),(2.1) при
![]() в различные моменты времени. Чтобы еще раз подчеркнуть отличие диффузионно-волнового уравнения от аналогичного волнового
в различные моменты времени. Чтобы еще раз подчеркнуть отличие диффузионно-волнового уравнения от аналогичного волнового
Из графиков видно, что решение диффузионно-волнового уравнения затухает со временем, что обусловлено наличием диффузионных эффектов в уравнении (1.1).