§ 7. Общая задача нелинейного программирования

Здесь в соответствии со схемой предыдущего параграфа рассматривается общая задача нелинейного программирования с гладкими функциями.

7.1. Постановка задачи.

Общей задачей нелинейной условной оптимизации мы будем называть условную задачу минимизации

f0(x) → min,   x ∈ Ω,

(1)

где Ω выделяется как ограничениями типа равенств

fi(x) = 0,   i = 1, ..., k,

(2)

так и ограничениями типа неравенств

gj(x) ≤ 0,   j = 1, ..., l

(3)

(см. рис. 22).

Рис. 22.

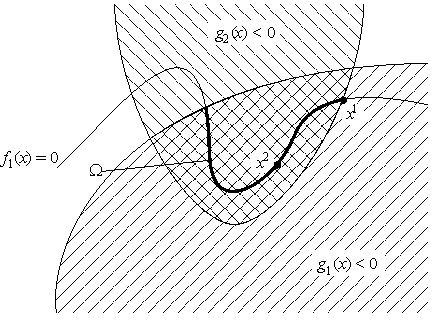
Как и в предыдущем параграфе определяются допустимые точки, локальный и глобальный, строгий и нестрогий минимумы. Так же мы будем использовать обозначения f и g для функций из R^m в R^k и R^l, соответственно, определяемые координатами f_i и g_j. Поэтому задачу (1)–(3) можно записывать в виде

f0(x) → min,   f(x) = Θ,   g(x) ≤ Θ.

(4)

(напомним, что неравенство g(x) ≤ Θ означает покоординатные неравенства).

Нам также потребуется следующее обозначение: a₊ = (a + |a|)/2; таким образом, a₊ = a, если a ≥ 0 и a₊ = 0, если a ≤ 0. Для векторов a ∈ R^m операция "+" определяется покоординатно: a₊ = ((a₁)₊, ..., (a_m)₊). Кроме того, через J(x) будет обозначаться множество индексов так называемых активных ограничений: J(x) = {j ∈ {1, ..., l}: g_j(x) = 0} — это номера ограничений, которые в данной точке существенны. Например, на рис. 22 J(x¹) = {2}, а J(x²) = ∅.

7.2. Теорема (обобщенное правило множителей Лагранжа).

Пусть f₀, f, g ∈ C¹, а x* — локальное решение задачи (4). Тогда найдутся такие λ*₀ ∈ R, λ* ∈ R^k, μ* ∈ R^l, не равные одновременно нулю, такие, что μ*_j ≥ 0 при j ∈ J(x*) и

λ*0 f ′0(x*)+  k ∑ i = 1 λ*i f ′i(x*)+    ∑ j∈J(x*) μ*j g′j(x*) = Θ.

(5)

Д о к а з а т е л ь с т в о.  Возьмем r > 0 таким, чтобы x* = argmin_x∈Ωr f(x), где Ω_r = Ω ∩ B(x*, r). Для любого n ∈ N определим функцию f ⁿ: R^m → R равенством

f n(x) = f0(x) + n(||f(x)||2 + ||g+(x)||2) + ||x – x*||2.

З а д а ч а   7.1. Докажите, что f ⁿ ∈ C¹, в частности, покажите, что (||g₊(x)||²)′ = 2g₊(x)g′(x).

Поскольку f ⁿ непрерывно дифференцируемы и поэтому непрерывны, функции f ⁿ на шаре B(x*, r) достигают минимума; обозначим его через xⁿ. В частности,

f n(xn) ≤ f n(x*),

(6)

т. е.

f0(xn) + n(||f(xn)||2 + ||g+(xn)||2) + ||xn – x*||2 ≤ f n(x*).

Отсюда, поскольку, как легко видеть, f ⁿ(x*) = f₀(x*),

||f(xn)||2 + ||g+(xn)||2 ≤  1 n [f0(x*) – ||xn – x*||2 – f0(xn)],

Выражение в квадратных скобках ограничено, так как xⁿ ∈ B(x*, r). Поэтому ||f(xⁿ)||² + ||g₊(xⁿ)||² → 0 при n → ∞ и, следовательно, f(xⁿ) → Θ и g₊(xⁿ) → Θ при n → ∞.

Пусть теперь {xni} — произвольная сходящаяся, скажем к y, подпоследовательность. Тогда, как легко видеть, во-первых, y ∈ Ω и, во-вторых, f ni(xni) → f0(y) + ||y – x*||2 при n → ∞. Поэтому, подставляя в (6) ni вместо n и переходя к пределу в получившемся неравенстве при i → ∞, получим

f0(y) + ||y – x*||2 ≤ f0(x*).

С другой стороны, так как x* = argmin f(x), f₀(x*) ≤ f₀(y). Отсюда ||y – x*||² ≤ 0, т. е. y = x*. Таким образом, любая сходящаяся подпоследовательность последовательности {xⁿ} сходится к x*. Последнее, учитывая компактность последовательности, гарантирует ее сходимость к тому же пределу.

Далее, в силу доказанного можно считать, что при всех n точка xⁿ лежит внутри шара B(x*, r). Поэтому в силу теоремы Ферма (f ⁿ)′(xⁿ) = Θ, т. е.

f ′0(xn)+ 2 k ∑ i = 1 fi(xn)f ′i(xn)+ 2 l ∑ j = 1 [gj(xn)]+g′j(xn)+ 2(xn – x*) = Θ.

(7)

Положим теперь

sn =  ( 1 + 4n2 k ∑ i = 1 [fi(xn)]2 + 4n2 l ∑ j = 1 [gj(xn)]2 ) –1/2 ,

λn0 = sn, λni= 2nfi(xn)sn, μnj= 2n[gj(xn)]+sn. Поскольку λn0,λnj,μnj∈ [–1, 1] (n ∈ N; i = 1, ..., k; j = 1, ..., l), можно считать, не ограничивая общности, что найдутся такие λ*0,λ*iи μ*j,что

λn0→ λ*0,  λni→ λ*i,  μnj→ μ*j  при  n → ∞.

Умножив (7) на sⁿ и переходя в получившемся равенстве к пределу при n → ∞, получаем

λ*0f ′0(x*)+  k ∑ i = 1 λ*if ′i(x*)+  l ∑ j = 1 μ*jg′j(x*)= Θ.

(8)

Остается заметить, что, во-первых, так как |λn0|2+ ∑ki=1|λni |2+∑lj=1|μnj|2=1, не все из λ*0,λ*i,μ*jравны нулю, во-вторых, поскольку μnj= 2n[gj(xn)]+sn ≥ 0, неотрицательны и μ*jи, наконец, в-третьих, если j ∉ J(x*) (т. е. gj(x*) < 0), то gj(xn) < 0 при больших n; поэтому [gj(x*)]+ = 0, что влечет равенство μ*j= 0 и, следовательно, равенство

l ∑ j = 1 μ*jg′j(x*)=    ∑ j∈J(x*) μ*jg′j(x*).

Таким образом (8) — это (5).

7.3. Регулярный случай.

Так же, как и в случае ограничений-равенств в случае общей задачи нелинейной оптимизации, необходимый признак, задаваемый теоремой 7.2, информативен только в случае, если λ*0≠ 0. В этой ситуации, так же как и в предыдущем параграфе можно разделить (5) на λ*0 и, следовательно, считать его равным единице. Это позволяет ввести функцию Лагранжа L: Rm×Rk×Rk → R (в регулярном случае) равенством

L(x, λ, μ) = f0(x) + (λ, f(x)) + (μ, g(x)).

Условие регулярности в случае общей задачи выглядит сложнее. Именно, допустимая точка x называется регулярной, если векторы f ′₁(x),..., f ′_k(x)линейно независимы и для некоторого ненулевого вектора h ∈ R^m

(f ′i(x),h) = 0 при i = 1, ..., k

и

(g′j(x),h) < 0 при j ∈ J(x).

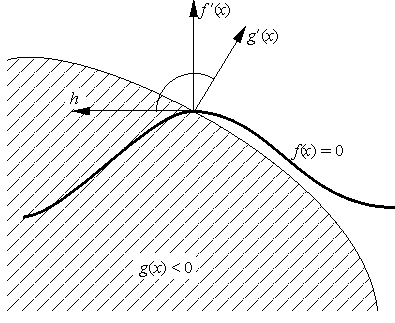
Геометрически, эти условия означают, что, во-первых, вектор h является касательным к многообразию, выделяемому ограничениями-равенствами (т. е. ортогонален всем градиентам f ′i(x)),и, во-вторых, он образует с градиентами g′j(x)активных ограничений (указывающими, очевидно, вовне множества Ω) тупой угол (см. рис. 23).

Рис. 23.

7.4. Теорема (обобщенное правило множителей Лагранжа в регулярном случае).

Пусть f₀, f, g ∈ C¹, а x* — регулярное локальное решение задачи (4). Тогда найдутся λ* ∈ R^k, μ* ∈ R^l не равные одновременно нулю, такие, что μ*_j ≥ 0 при j ∈ J(x*) и

L′x(x*,λ*, μ*) = 0,

(9)

(μ*, g(x*)) = 0.

(10)

Д о к а з а т е л ь с т в о.  Пусть λ0**, λ** и μ** — величины, существование которых утверждается в теореме 7.2. Покажем, что λ0** ≠ 0. В предположении противного умножим (5) скалярно на вектор h, фигурирующий в определении регулярности x*:

k ∑ i = 1 λi**(f ′i(x*),h)+    ∑ j∈J(x*) μj**(g′j(x*),h) = Θ.

(11)

В силу регулярности (f ′i(x*),h) = 0 и (g′j(x),h) < 0, а по теореме 7.2 μj**≥ 0 при j ∈ J(x*). Поэтому (11) влечет равенство μ** = Θ. Но тогда (5) означает, что

k ∑ i = 1 λi**f ′i(x*)= Θ,

что вместе с линейной независимостью f ′i(x*)дает равенство λ** = Θ. Противоречие.

Таким образом λ₀**≠ 0. Положим теперь λ*_i= λ_i**/λ₀**(i = 1, ..., k),

μ*j=  { μj**/λ0**при  j ∈ J(x*), 0  при  j ∉ J(x*).

Очевидно теперь, (10) выполняется автоматически, а (9) тривиально получается из (5).

7.5. Достаточные условия, существование, единственость.

Ситуация с задачей (1)–(3) несколько отличается от изучавшихся ранее, поскольку минимумы здесь могут быть двух типов. В случае, когда в точке минимума x* нет активных ограничений, т. е. J(x*) = ∅, ситуация полностью аналогична описанной в предыдущем параграфе, поскольку ограничения-неравенства в окрестности точки x* можно опустить (см. рис. 24а). В случае же, когда J(x*) ≠ ∅ минимум может достигаться на границе множества Ω и точка x* может не быть стационарной точкой (см. рис. 24б).

Рис. 24.

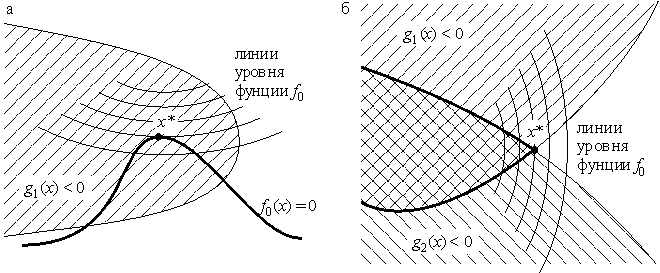
Мы ограничимся лишь формулировками результатов, поскольку в идейном плане они не доставляют ничего нового. Аналогом теоремы 6.9 может служить следующая

Теорема (достаточные условия минимума). Пусть f₀, f, g ∈ C², а x* — допустимая точка такая, что для некоторых λ* ∈ R^k и μ* ∈ R^l, одновременно не равных нулю, выполнены условия (9)–(10) и при любых h ∈ R^m, h ≠ Θ таких, что

(f ′i(x*),h) = 0  при  i = 1, ..., k; (g′j(x*),h) = 0  при  j ∈ J(x*), μ*j> 0; (g′j(x*),h) ≥ 0  при  j ∈ J(x*), μ*j= 0

выполнено неравенство (L′′xx(x*,λ*, μ*)h, h) > 0. Тогда x* — локальное решение задачи (1)–(3).

З а д а ч а  7.2. Докажите.

Что касается утверждений о существовании и единственности, то ситуация с результатами, которые могут быть доказаны изученными выше приемами, полностью аналогична.

З а д а ч а  7.3. Сформулируйте и докажите аналоги утверждений задач 6.7 и 6.8 для задачи (1)–(3).

7.6. Об ограничениях-равенствах.

С целью упрощения изложения, начиная с этого момента, мы будем рассматривать задачу условной оптимизации, содержащую только ограничения-неравенства. Это, с одной стороны, не снижает общности изложения, поскольку ограничения-равенства сводятся к ограничениям-неравенствам: ограничение

f(x) = Θ

эквивалентно ограничениям

f(x) ≤ Θ,   –f(x) ≤ Θ.

С другой стороны, задачи с ограничениями-равенствами мы уже достаточно подробно рассматривали выше.

Здесь, правда, следует помнить об одном важном обстоятельстве. При решении задач с ограничениями-неравенствами часто бывает важна (существенно используется) выпуклость функций, фигурирующих в задаче, вернее, выпуклость минимизируемой функции f₀ и выпуклость множества Ω допустимых точек. Последнее гарантируется выпуклостью функций g_j в ограничениях-неравенствах (см. задачу 7.4 ниже). Множества же, выделяемые ограничениями-равенствами, не бывают выпуклыми, за исключением случая аффинных функций f_i. Поэтому методы решения задач условной оптимизации, существенно использующие "выпуклость задачи" могут применяться к задачам с ограничениями-равенствами с большой осторожностью.

Напомним, что множество Ω ⊂ R^m называется выпуклым, если ∀(x, y ∈ Ω, λ ∈ [0, 1])[λx + (1 – λ)y ∈ Ω].

З а д а ч а  7.4. Докажите, что если функции g_i: R^m → R (i = 1, ..., l) выпуклы, то множество Ω = {x ∈ R^m: g_i(x) ≤ 0, i = 1, ..., l} выпукло.

З а д а ч а  7.5. Докажите, что если функция g: R^m→ R выпукла, вместе с функцией –g, то она аффинна: g(x) = (b, x) + c.

7.7. Еще один достаточный признак условного минимума.

Напомним, что точка (x*, λ*) называется седловой точкой функции L: Ω₁×Ω₂ → R (Ω₁ ⊂ R^m, Ω₂ ⊂ R^l), если при всех (x, λ) ⊂ Ω₁×Ω₂ выполнены неравенства

L(x*, λ) ≤ L(x*, λ*) ≤ L(x, λ*)

Теорема. Пусть (x*, λ*) — седловая точка функции Лагранжа L: Rm×Rl+→ R задачи (1), (3) (здесь Rl+= {λ ∈ Rl: λ ≥ Θ}), λ* ≥ Θ, x* — допустимая точка. Тогда x* — глобальное решение этой задачи.

Д о к а з а т е л ь с т в о.  Пусть x — произвольная допустимая точка, т. е. g_i(x) ≤ 0 (i = 1, ..., l). Тогда

f0(x*) + (λ*, g(x*)) = L(x*, λ*) ≤ L(x, λ*) = f0(x) +(λ*, g(x)).

(12)

Покажем, что

(λ*, g(x*)) = 0.

(13)

Тогда из (12), поскольку λ* ≥ Θ, а g(x) ≤ Θ, будет следовать нужное неравенство f₀(x*) ≤ f₀(x). Для доказательства (13) заметим, что по условию теоремы L(x*, Θ) ≤ L(x*, λ*), т. е.

(λ*, g(x*)) ≥ 0.

(14)

Равенство (13) вытекает теперь из (14), т.к. λ* ≥ Θ, а g(x*) ≤ Θ.

Тот факт, что доказанная теорема дает лишь достаточный признак условного минимума демонстрируетсмя в следующей задаче.

З а д а ч а  7.6. Покажите, что одномерная задача минимизации функции f(x) = –x при ограничениях x ≤ 1, –x ≤ 0 разрешима, но ее функция Лагранжа не имеет седловых точек.

З а д а ч а  7.7. Если в предыдущей теореме (x*, λ*) — локальная седловая точка, то можно ли утверждать, что x* — локальное решение задачи (1), (3)? (Ответ: нельзя).

Однако, если функции f₀ и g_i (i = 1, ..., l) выпуклы, а множество Ω содержит хотя бы одну внутреннюю точку, то условия доказанной теоремы являются необходимыми и достаточными (это утверждение называется теоремой Куна — Таккера; оно является центральным фактом теории выпуклого программирования).

Перейдем к описанию методов решения задач с ограничениями-неравенствами. Многие из описываемых ниже методов либо существенно используют выпуклость объектов, фигурирующих в задаче, либо вообще неработоспособны на невыпуклых задачах.

7.8. Методы возможных направлений.

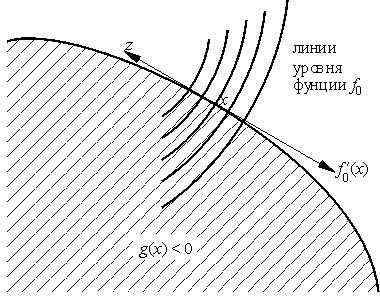
Эти методы основываются на следующем простом понятии. Вектор (направление) z в допустимой точке x назовем возможным для задачи (1), (3), если малое перемещение в этом неправлении уменьшает значение функции f₀ и не выводит из множества допустимых точек, т. е. если при достаточно малых s точка x^s = x + sz допустима и f(x^s) < f(x). Если теперь на каждом шаге сдвигаться в возможном направлении на достаточно малое расстояние, то мы очевидно получим релаксационную последовательность, которая во многих случаях будет сходиться к решению задачи. Методы этого типа называются методами возможных направлений.

З а д а ч а  7.8*. Докажите, что если (f₀(x), z) < 0, то малое перемещение из точки x в направлении z уменьшает значение функции f₀ (ср. с доказательством теоремы Ферма).

З а д а ч а  7.9*. Докажите, что если точка x допустима и (g_i(x), z) < 0 при i ∈ J(x), то малое перемещение из точки x в направлении z не выводит из множества допустимых точек.

В силу этих задач возможное направление zⁿ в очередной точке xⁿ, в котором функция f₀ будет убывать быстрее всего, можно искать, решая задачу линейного программирования (о методах решения линейных задач см. список литературы)

(f ′0(xn),z) → min,

(15)

(g′i(xn),z) ≤ 0,   i ∈ J(xn),

(16)

zi – 1 ≤ 0,   –zi – 1 ≤ 0,   i = 1, ..., m.

(17)

Здесь "нормализующие" ограничения (16) введены для того, чтобы искать вектор возможных направлений на ограниченном множестве, т. е. для того, чтобы линейная задача (15)–(16) была разрешима. К сожалению, решение задачи (15)–(16) не всегда дает возможное направление (см. рис. 25). Причиной этого являются нестрогие неравенства в (16) (задачи же со строгими неравенствами часто оказываются неразрешимыми, поскольку точная нижняя грань значений функции f₀ часто достигается на границе множества допустимых точек, которая в случае строгих ограничений-неравенств не принадлежит этому множеству). Эту трудность можно обойти разными способами. Например, на каждом шаге можно "возвращать" точку во множество Ω с помощью какой-либо процедуры "проектирования" см., например, следующий пункт). Можно также поступать следующим образом. Для любой допустимой точки x и произвольного ε > 0 определим множество J_ε(x) индексов так называемых ε-активных ограничений:

Jε(x) = {i ∈ {1, ..., m}: gi(x) ≥ –ε}.

Рис. 25.

Таким образом, если ε малó и i ∈ J_ε(x), то i-ое ограничение в точке x почти обращается в равенство. В одном из вариантов метода возможных направлений выбирают последовательность ε_n → 0 и из очередной точки xⁿ следующий шаг совершют в направлении zⁿ:

xn+1 = xn + αnzn,

(18)

где zⁿ есть решение следующей линейной задачи

ξ→ min

с ограничениями

(f ′0(xn),z) – ξ ≤ 0,

(g′i(xn),z) – ξ ≤ 0,   i ∈ Jεn(xn)

и нормализующими ограничениями (16). Подчеркнем, что в этой задаче неизвестными являются z и ξ. Длина шага в (18) выбирается таким образом, чтобы точка xⁿ⁺¹ не выходила из множества допустимых точек.

7.9. Методы проекции градиента.

Проекцией P_Ωx точки x ∈ R^m на множество Ω ⊂ R^m называется любая ближайшая к x точка множества Ω:

||x – PΩx|| ≤ ||x – y|| при всех y ∈ Ω.

З а д а ч а  7.10. Докажите, что если Ω замкнуто и выпукло, то для любой точки проекция сужествует и единственна.

З а д а ч а  7.11. Приведите пример, когда проекция: а) не существует; б) не единственна.

В тех случаях, когда проекцию точки на множество допустимых точек задачи (1), (3) найти достаточно легко (например, когда Ω — линейное подпространство, полупространство, шар, Rm+и  т. д.) используют метод проекции градиента:

xn+1 = PΩ(xn – αnf ′0(xn))

(см. рис. 26), являющийся прямым обобщением градиентного метода.

Рис. 26.

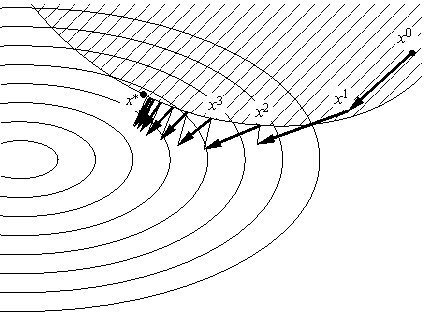
Можно доказать, например, что если функция f₀ ∈ C¹ сильно выпукла и f ′ удовлетворяет условию Липшица, а множество Ω замкнуто и ограничено, то метод проекции градиента сходится со скоростью геометрической прогрессии.

7.10. Методы линеаризации.

Суть этих методов, как следует из названия, состоит в линеаризации минимизируемой функции и ограничений в очередной точке xⁿ строящейся релаксационной последовательности и объявлении следующим значением xⁿ⁺¹ решения получающейся линейной задачи, т. е. задачи

(f ′0(xn),x – xn) → min,

(19)

gi(xn) + (g′i(xn),x – xn) ≤ 0,   i = 1, ..., l.

(20)

Чтобы эта (линейная) задача была разрешима либо добавляют штраф в минимизируемую функцию, заменяя (19), например, задачей

(f ′0(xn), x– xn) + δ||x – xn||2 → min,

либо добавляя к (20) простые ограничения, которые делают множество допустимых точек этой задачи ограниченным, например, (линейные) ограничения

xi – xni– αn ≤ 0,   –xi + xni– αn ≤ 0   (i = 1, ..., m).

Часто для уменьшения объема вычислительной работы среди ограничений (20) оставляют только ε-активные.

7.11. Методы штрафов.

Основная идея здесь заключается в переходе от задачи (1), (3) к задаче безусловной оптимизации, в которой "наказывается" либо удаление от множества Ω допустимых точек (внешний штраф), либо приближение изнутри множества Ω к его границе (внутренний штраф). Например, это можно сделать так. Для любого s > 0 определим функцию Fsout:Rm → R равенством (индекс "out" станет понятен чуть ниже)

Fsout(x)= f0(x) + s l ∑ i = 1 (gi)2+(x).

(21)

З а д а ч а  7.12 (ср. с задачей 6.11). Пусть f₀, g ∈ C¹, а x* — единственное решение задачи (1), (3). Пусть, кроме того, множество {x ∈ R^m: ||g_i(x)|| ≤ ε, i = 1, ..., l} при некотором ε ≥ 0 непусто и ограничено. Докажите, что (безусловная) задача

F sout(x)→ min

(22)

при всех s разрешима и ее решение x^s сходится к x* при s→ ∞.

Геометрическая трактовка замены задачи (1), (3) задачей (22) изображена на рис. 27.

Рис. 27.

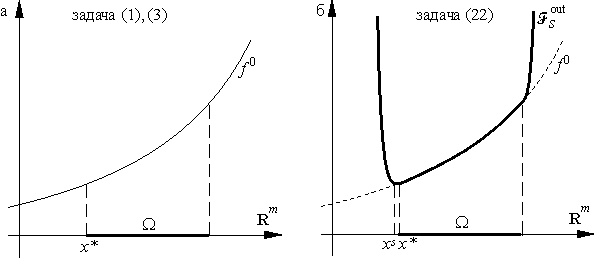
Задачу (22) решают тем или иным методом решения безусловных задач, увеличивая на каждом шаге штраф s. Как и в случае задач с ограничениями-равенствами, основным недостатком метода штрафов является рост числа обусловленности задачи (22) с ростом s.

Описанный класс методов называют методами внешних штрафов, поскольку минимизируемая функция изменяется вне множества Ω. На несколько другой идее основываются так называемые методы внутренних штрафов или барьеров. Образно его можно описать так: у границы множества Ω возводятся барьеры, не позволяющие приближаться к его границе. Например, вместо задачи (1), (3) можно рассмотреть задачу

Fsin(x)→ min,

(23)

где функция Fsin: Ωg →R определяется равенством (ср. с ((21))

Fsin(x)= f0(x) + s l ∑ i = 1 1 gi(x) .

Сравнение геометрических интерпретаций задач (1), (3) и (23) изображено на рис. 28.

Рис. 28.

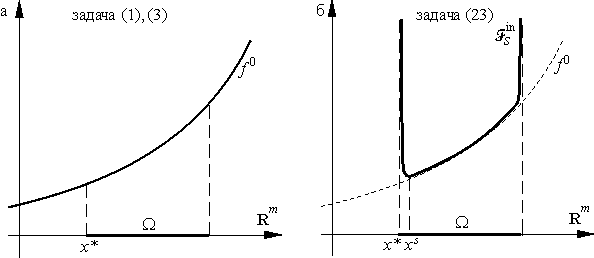
З а д а ч а  7.13. Сформулируйте и докажите аналог задачи 7.5 для метода барьеров.

Задача (23) решается методами, развитыми для безусловных задач; при этом "крутизна барьера" характеризуемая числом s, возрастает на каждом шаге.

З а д а ч а  7.14. Попытайтесь выписать аналоги штрафных функций Fsoutи Fsinдля общей задачи нелинейного программирования (1)–(3), содержащей как ограничения-неравенства, так и ограничения-равенства.

7.12. Двойственные методы.

Суть методов из этого весьма обширного класса в применении к задачам с ограничениями-неравенствами, так же как и в задачах с ограничениями-равенствами, заключается в замене условной задачи (1), (3) задачей поиска стационарной (часто седловой) точки функции Лагранжа. В выпуклом случае задача (1), (3) и задача о поиске седловой точки функции Лагранжа в силе теоремы Куна – Таккера эквивалентны. Например, применение простейшего (градиентного) метода к последней задаче приводит к следующему методу Эрроу – Гурвица – Удзавы:

xn+1 = xn – αnL′x(xn,μn), μn+1 = [μn + αnL′μ(xn,μn)]+.

Для поиска седловой точки в двойственных методах применяют почти весь спектр описанных выше методов минимизации — методы Ньютона, квазиньютоновские методы, методы сопряженных направлений и  т. д.

File based on translation from T_EX by T_TH, version 3.05.
Created 10 Jun 2001, 20:58.